Testing bilateral symmetry¶
This notebook describes a first pass at testing for some notion of bilateral symmetry. Here, we focus only on the left-left and right-right induced subgraphs for simplicity. We also use the unweighted version of the maggot connectomes. Also, for now, we restrict ourselves to the set of neurons for which we know a pairing between neuron A on the left hemisphere and neuron A on the right hemisphere.
To summarize, this notebook presents a strange phenomena where depending on the dimension of the embedding that we use to test bilateral symmetry, we get vastly different results.
We also present a modified proceedure that fails to reject the null that the latent positions of the left-left induced subgraph and the right-right induced subgraph have the same distribution over many embedding dimensions, suggesting that for the current setup we fail to reject bilateral symmetry.
Preliminaries¶
from pkg.utils import set_warnings
set_warnings()
import datetime
import pprint
import time
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from hyppo.ksample import KSample
from scipy.stats import epps_singleton_2samp, ks_2samp
from graspologic.align import OrthogonalProcrustes, SeedlessProcrustes
from graspologic.embed import AdjacencySpectralEmbed, select_dimension
from graspologic.plot import pairplot
from graspologic.utils import (
augment_diagonal,
binarize,
multigraph_lcc_intersection,
pass_to_ranks,
)
from pkg.data import load_adjacency, load_node_meta
from pkg.io import savefig
from pkg.plot import set_theme
from pkg.utils import get_paired_inds, get_paired_subgraphs
from src.visualization import adjplot # TODO fix graspologic version and replace here
t0 = time.time()
def stashfig(name, **kwargs):
foldername = "bilateral_symmetry"
savefig(name, foldername=foldername, **kwargs)
colors = sns.color_palette("Set1")
palette = dict(zip(["Left", "Right", "OP", "O-SP"], colors))
set_theme()
/Users/bpedigo/miniconda3/envs/maggot-revamp/lib/python3.8/site-packages/umap/__init__.py:9: UserWarning: Tensorflow not installed; ParametricUMAP will be unavailable
warn("Tensorflow not installed; ParametricUMAP will be unavailable")
Load the data¶
Load node metadata and select the subgraphs of interest¶
meta = load_node_meta()
meta = meta[meta["paper_clustered_neurons"]]
adj = load_adjacency(graph_type="G", nodelist=meta.index)
lp_inds, rp_inds = get_paired_inds(meta)
left_meta = meta.iloc[lp_inds]
right_meta = meta.iloc[rp_inds]
ll_adj, rr_adj, lr_adj, rl_adj = get_paired_subgraphs(adj, lp_inds, rp_inds)
# TODO not sure what we wanna do about LCCs here
adjs, lcc_inds = multigraph_lcc_intersection([ll_adj, rr_adj], return_inds=True)
ll_adj = adjs[0]
rr_adj = adjs[1]
print(f"{len(lcc_inds)} in intersection of largest connected components.")
print(f"Original number of valid pairs: {len(lp_inds)}")
left_meta = left_meta.iloc[lcc_inds]
right_meta = right_meta.iloc[lcc_inds]
meta = pd.concat((left_meta, right_meta))
n_pairs = len(ll_adj)
print(f"Number of pairs after taking LCC intersection: {n_pairs}")
1148 in intersection of largest connected components.
Original number of valid pairs: 1149
Number of pairs after taking LCC intersection: 1148
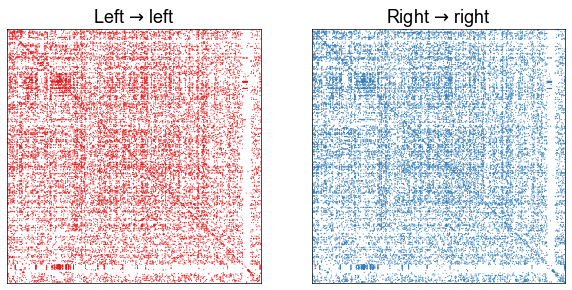
Plotting the aligned adjacency matrices¶
At a high level, we see that the left-left and right-right induced subgraphs look quite similar when aligned by the known neuron pairs.
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
adjplot(
ll_adj,
plot_type="scattermap",
sizes=(1, 2),
ax=axs[0],
title=r"Left $\to$ left",
color=palette["Left"],
)
adjplot(
rr_adj,
plot_type="scattermap",
sizes=(1, 2),
ax=axs[1],
title=r"Right $\to$ right",
color=palette["Right"],
)
stashfig("left-right-induced-adjs")
Embedding the graphs¶
Here I embed the unweighted, directed graphs using ASE.
def plot_latents(left, right, title="", n_show=4):
plot_data = np.concatenate([left, right], axis=0)
labels = np.array(["Left"] * len(left) + ["Right"] * len(right))
pg = pairplot(plot_data[:, :n_show], labels=labels, title=title)
return pg
def screeplot(sing_vals, elbow_inds, color=None, ax=None, label=None):
if ax is None:
_, ax = plt.subplots(1, 1, figsize=(8, 4))
plt.plot(range(1, len(sing_vals) + 1), sing_vals, color=color, label=label)
plt.scatter(
elbow_inds, sing_vals[elbow_inds - 1], marker="x", s=50, zorder=10, color=color
)
ax.set(ylabel="Singular value", xlabel="Index")
return ax
def embed(adj, n_components=40, ptr=False):
if ptr:
adj = pass_to_ranks(adj)
elbow_inds, elbow_vals = select_dimension(augment_diagonal(adj), n_elbows=4)
elbow_inds = np.array(elbow_inds)
ase = AdjacencySpectralEmbed(n_components=n_components)
out_latent, in_latent = ase.fit_transform(adj)
return out_latent, in_latent, ase.singular_values_, elbow_inds
Run the embedding¶
n_components = 8
max_n_components = 40
preprocess = "binarize"
if preprocess == "binarize":
ll_adj = binarize(ll_adj)
rr_adj = binarize(rr_adj)
left_out_latent, left_in_latent, left_sing_vals, left_elbow_inds = embed(
ll_adj, n_components=max_n_components
)
right_out_latent, right_in_latent, right_sing_vals, right_elbow_inds = embed(
rr_adj, n_components=max_n_components
)
Plot the screeplots¶
fig, ax = plt.subplots(1, 1, figsize=(8, 4))
screeplot(left_sing_vals, left_elbow_inds, color=palette["Left"], ax=ax, label="Left")
screeplot(
right_sing_vals, right_elbow_inds, color=palette["Right"], ax=ax, label="Right"
)
ax.legend()
ax.axvline(n_components, color="black", linewidth=1.5, linestyle="--")
stashfig(f"screeplot-preprocess={preprocess}")
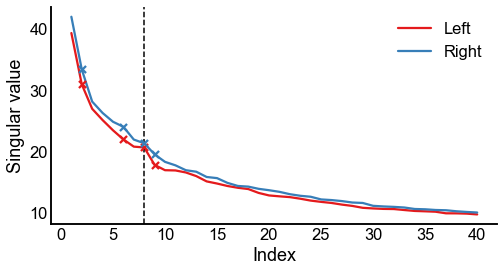
Calculating the Frobenius norm of the adjacency matrices¶
Note that in the screeplot above, the singular values of the right-right subgraph are always above those of the left-left subgraph (at least for this range of \(d\)). This hints as the “scale” of the two graphs. We’ve noticed that the left-left subgraph is slightly less dense than the right-right.
It is perhaps worth investigating whether to use the “scaled” version of the hypothesis test.
print(f"Norm of left-left adjacency: {np.linalg.norm(binarize(ll_adj))}")
print(f"Norm of right-right adjacency: {np.linalg.norm(binarize(rr_adj))}")
Norm of left-left adjacency: 163.6459593146131
Norm of right-right adjacency: 170.35551062410633
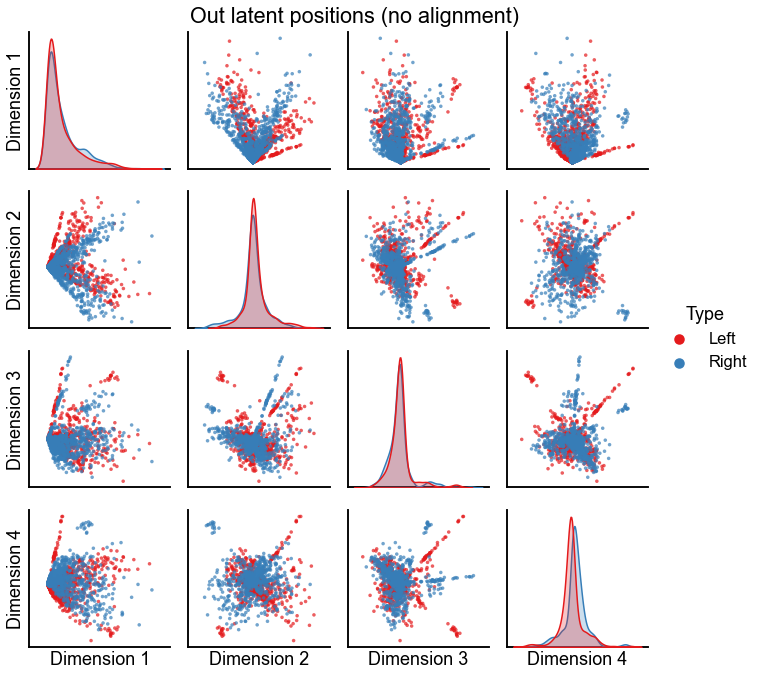
Plot the latent positions of both graphs before alignment¶
plot_latents(
left_out_latent, right_out_latent, title="Out latent positions (no alignment)"
)
stashfig(f"out-latent-no-align-preprocess={preprocess}")
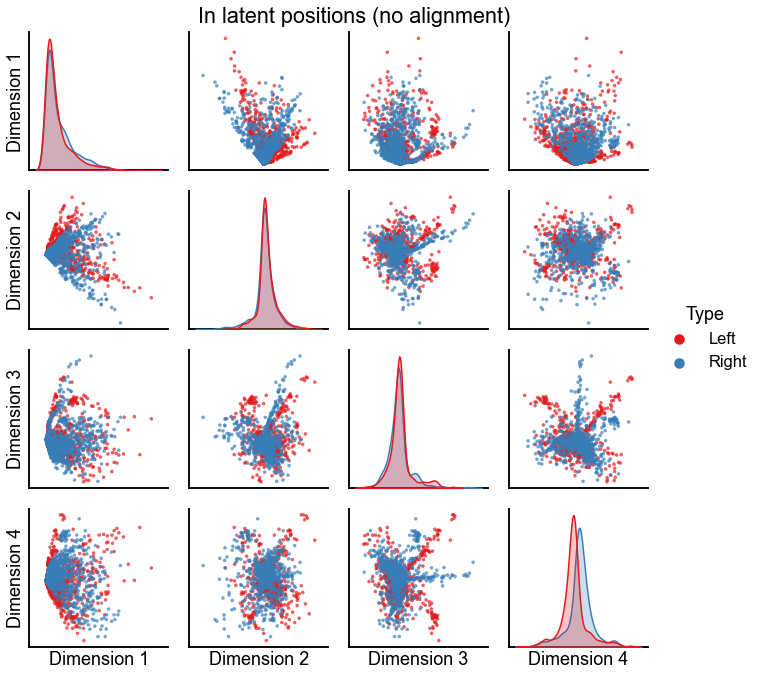
plot_latents(
left_in_latent, right_in_latent, title="In latent positions (no alignment)"
)
stashfig(f"in-latent-no-align-preprocess={preprocess}")
Align the embeddings¶
Here we align first using orthogonal Procrustes (OP), and then using seedless Procrustes initialized at the orthogonal Procrustes solution (O-SP).
I also calculate the Frobenius norm of the difference in the embeddings after performing the alignment.
def run_alignments(X, Y, scale=False):
X = X.copy()
Y = Y.copy()
if scale:
X_norm = np.linalg.norm(X, ord="fro")
Y_norm = np.linalg.norm(Y, ord="fro")
avg_norms = (X_norm + Y_norm) / 2
X = X * (avg_norms / X_norm)
Y = Y * (avg_norms / Y_norm)
op = OrthogonalProcrustes()
X_trans_op = op.fit_transform(X, Y)
sp = SeedlessProcrustes(init="custom", initial_Q=op.Q_)
X_trans_sp = sp.fit_transform(X, Y)
return X_trans_op, X_trans_sp
def calc_diff_norm(X, Y):
return np.linalg.norm(X - Y, ord="fro")
Plot the alignment for d=8 dimensions¶
n_components = 8
op_left_out_latent, sp_left_out_latent = run_alignments(
left_out_latent[:, :n_components], right_out_latent[:, :n_components]
)
op_diff_norm = calc_diff_norm(op_left_out_latent, right_out_latent[:, :n_components])
sp_diff_norm = calc_diff_norm(sp_left_out_latent, right_out_latent[:, :n_components])
print(f"Procrustes diff. norm using true pairs: {op_diff_norm:0.3f}")
print(f"Seedless Procrustes diff. norm using true pairs: {sp_diff_norm:0.3f}")
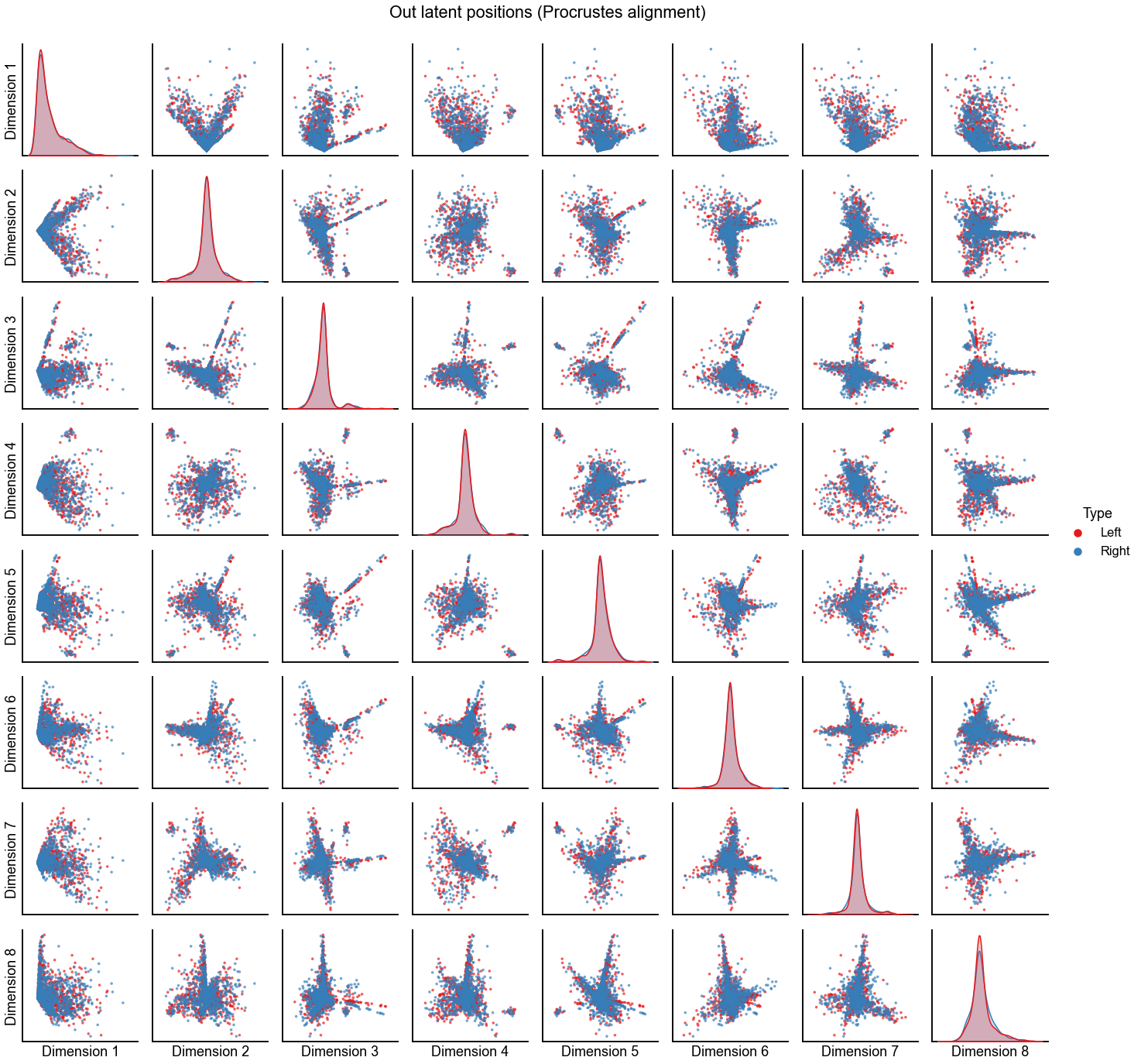
plot_latents(
op_left_out_latent,
right_out_latent[:, :n_components],
"Out latent positions (Procrustes alignment)",
n_show=n_components,
)
stashfig(f"out-latent-op-preprocess={preprocess}")
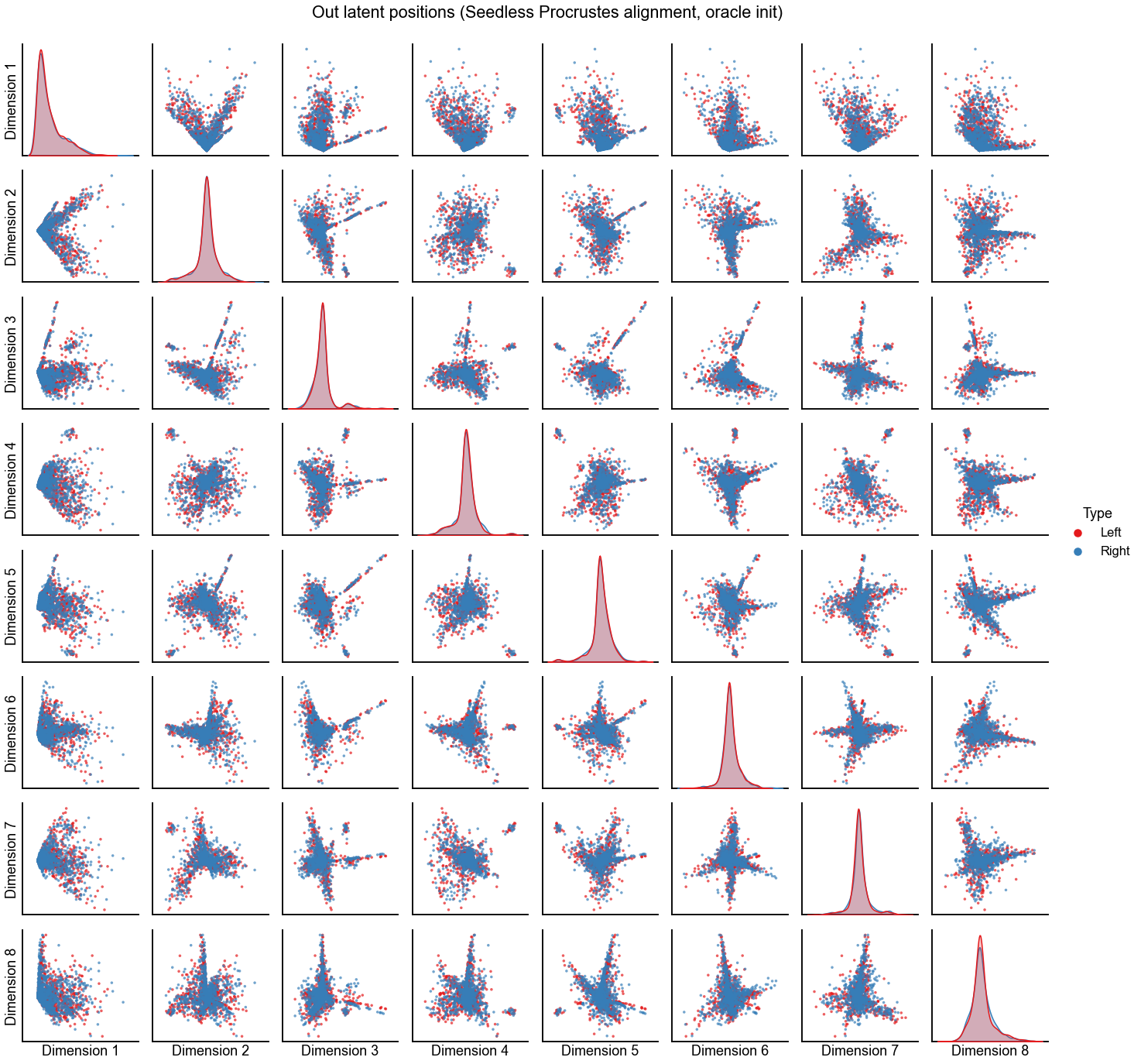
plot_latents(
sp_left_out_latent,
right_out_latent[:, :n_components],
"Out latent positions (Seedless Procrustes alignment, oracle init)",
n_show=n_components,
)
stashfig(f"out-latent-o-sp-n_components={n_components}-preprocess={preprocess}")
Procrustes diff. norm using true pairs: 4.732
Seedless Procrustes diff. norm using true pairs: 4.789
Plot the alignment for d=7 dimensions¶
n_components = 7
op_left_out_latent, sp_left_out_latent = run_alignments(
left_out_latent[:, :n_components], right_out_latent[:, :n_components]
)
op_diff_norm = calc_diff_norm(op_left_out_latent, right_out_latent[:, :n_components])
sp_diff_norm = calc_diff_norm(sp_left_out_latent, right_out_latent[:, :n_components])
print(f"Procrustes diff. norm using true pairs: {op_diff_norm:0.3f}")
print(f"Seedless Procrustes diff. norm using true pairs: {sp_diff_norm:0.3f}")
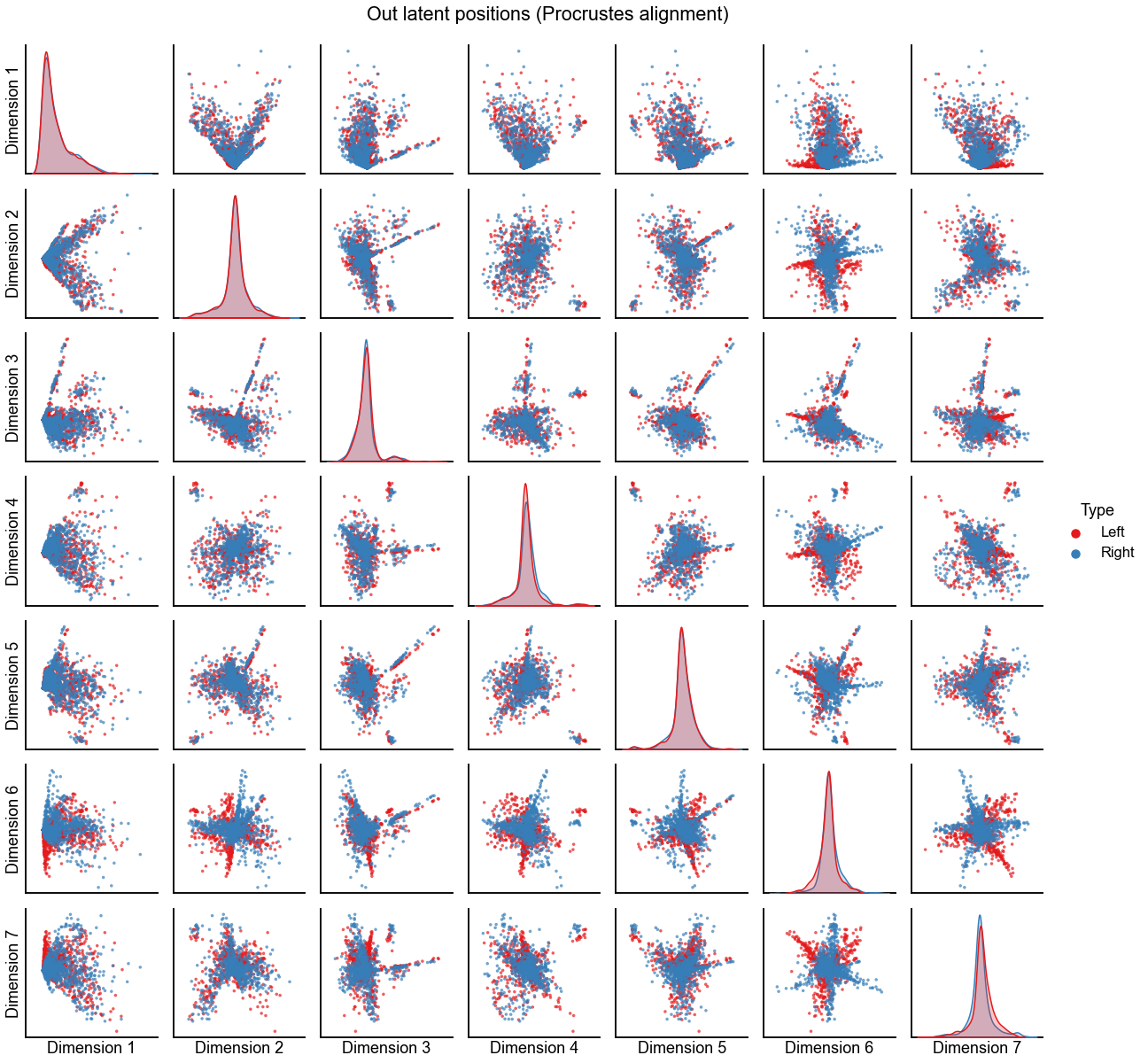
plot_latents(
op_left_out_latent,
right_out_latent[:, :n_components],
"Out latent positions (Procrustes alignment)",
n_show=n_components,
)
stashfig(f"out-latent-op-preprocess={preprocess}")
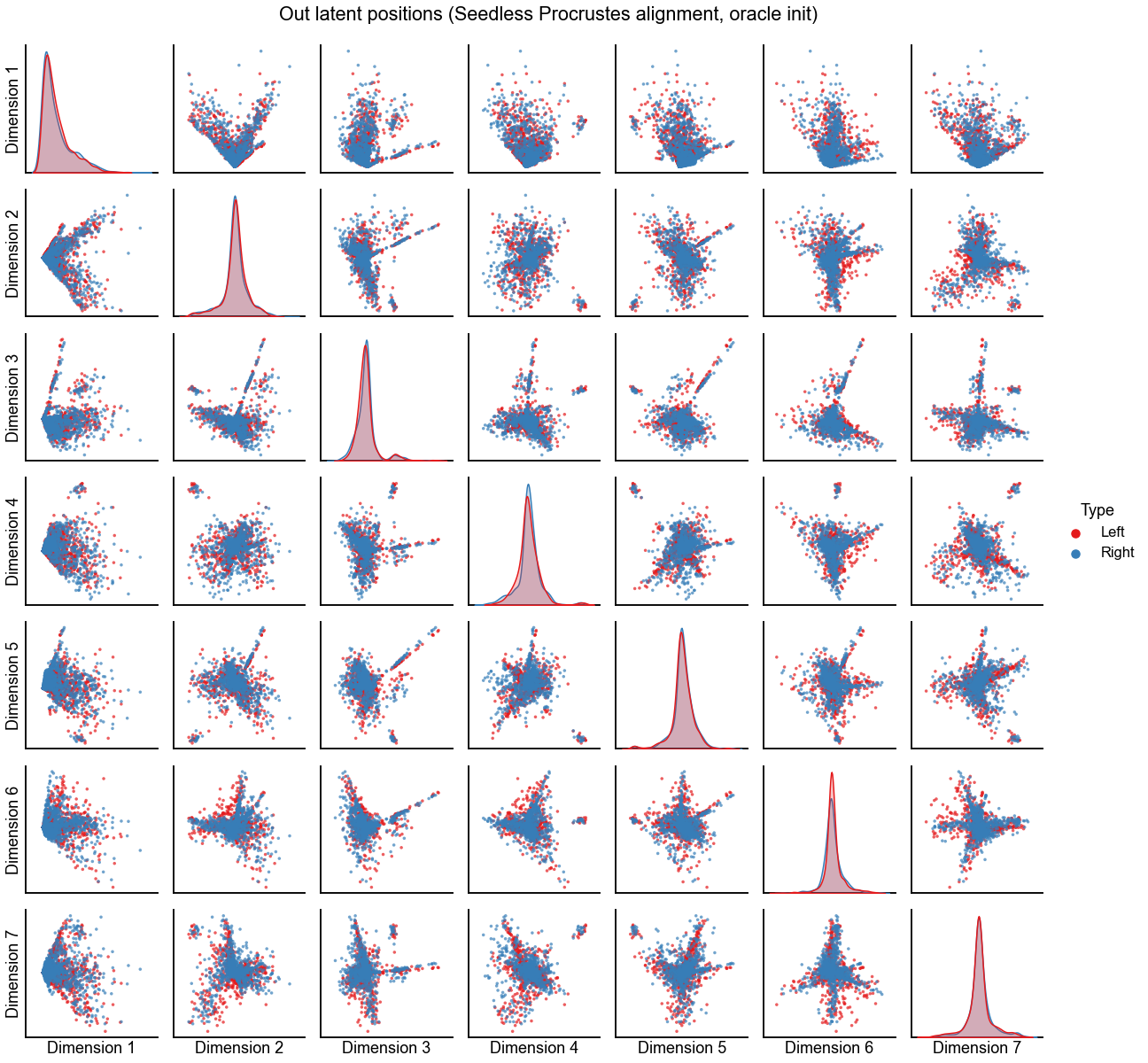
plot_latents(
sp_left_out_latent,
right_out_latent[:, :n_components],
"Out latent positions (Seedless Procrustes alignment, oracle init)",
n_show=n_components,
)
stashfig(f"out-latent-o-sp-n_components={n_components}-preprocess={preprocess}")
Procrustes diff. norm using true pairs: 7.238
Seedless Procrustes diff. norm using true pairs: 9.052
Hypothesis testing on the embeddings¶
To test whether the distribution of latent positions is different, we use the approach of the “nonpar” test, also called the latent distribution test. Here, for the backend 2-sample test, we use distance correlation (Dcorr).
test = "dcorr"
workers = -1
auto = True
if auto:
n_bootstraps = None
else:
n_bootstraps = 500
def run_test(
X1,
X2,
rows=None,
info={},
auto=auto,
n_bootstraps=n_bootstraps,
workers=workers,
test=test,
print_out=False,
):
currtime = time.time()
test_obj = KSample(test)
tstat, pvalue = test_obj.test(
X1,
X2,
reps=n_bootstraps,
workers=workers,
auto=auto,
)
elapsed = time.time() - currtime
row = {
"pvalue": pvalue,
"tstat": tstat,
"elapsed": elapsed,
}
row.update(info)
if print_out:
pprint.pprint(row)
if rows is not None:
rows.append(row)
else:
return row
Run the two-sample test for varying embedding dimension¶
rows = []
for n_components in np.arange(1, 21):
op_left_out_latent, sp_left_out_latent = run_alignments(
left_out_latent[:, :n_components], right_out_latent[:, :n_components]
)
op_left_in_latent, sp_left_in_latent = run_alignments(
left_in_latent[:, :n_components], right_in_latent[:, :n_components]
)
op_left_composite_latent = np.concatenate(
(op_left_out_latent, op_left_in_latent), axis=1
)
sp_left_composite_latent = np.concatenate(
(sp_left_out_latent, sp_left_in_latent), axis=1
)
right_composite_latent = np.concatenate(
(right_out_latent[:, :n_components], right_in_latent[:, :n_components]), axis=1
)
run_test(
op_left_composite_latent,
right_composite_latent,
rows,
info={"alignment": "OP", "n_components": n_components},
)
run_test(
sp_left_composite_latent,
right_composite_latent,
rows,
info={"alignment": "O-SP", "n_components": n_components},
)
results = pd.DataFrame(rows)
Plot the 2-sample test p-values by varying dimension¶
Note: these are on a log y-scale.
def plot_pvalues(results, line_locs=[0.05, 0.005, 0.0005]):
results = results.copy()
# jitter so we can see op vs o-sp
op_results = results[results["alignment"] == "OP"]
sp_results = results[results["alignment"] == "O-SP"]
results.loc[op_results.index, "n_components"] += -0.15
results.loc[sp_results.index, "n_components"] += 0.15
styles = ["-", "--", ":"]
line_kws = dict(color="black", alpha=0.7, linewidth=1.5, zorder=-1)
# plot p-values by embedding dimension
fig, ax = plt.subplots(1, 1, figsize=(10, 6))
sns.scatterplot(
data=results,
x="n_components",
y="pvalue",
hue="alignment",
palette=palette,
ax=ax,
s=40,
)
ax.set_yscale("log")
styles = ["-", "--", ":"]
line_kws = dict(color="black", alpha=0.7, linewidth=1.5, zorder=-1)
for loc, style in zip(line_locs, styles):
ax.axhline(loc, linestyle=style, **line_kws)
ax.text(ax.get_xlim()[-1] + 0.1, loc, loc, ha="left", va="center")
ax.set(xlabel="Dimension", ylabel="p-value")
ax.get_legend().remove()
ax.legend(bbox_to_anchor=(1.15, 1), loc="upper left", title="Alignment")
xlim = ax.get_xlim()
for x in range(1, int(xlim[1]), 2):
ax.axvspan(x - 0.5, x + 0.5, color="lightgrey", alpha=0.2, linewidth=0)
plt.tight_layout()
plot_pvalues(results)
stashfig(
f"naive-pvalues-test={test}-n_bootstraps={n_bootstraps}-preprocess={preprocess}"
)
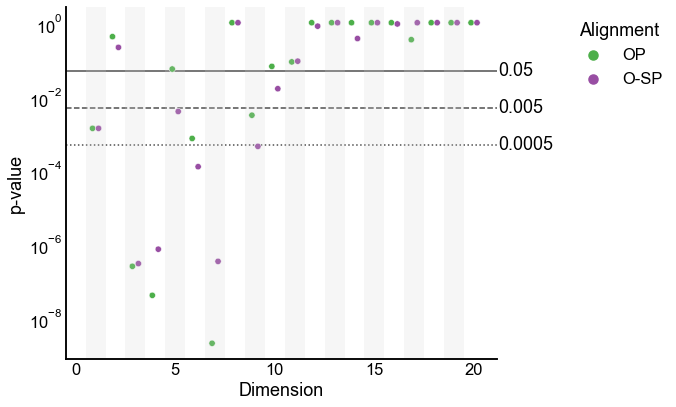
Not what we expected¶
It is worrisome that the p-values change drastically when the embedding dimension changes slightly.
Below, we investigate what could be causing this phenomenon.
Focus on the d=1 case¶
Note that in the testing above, even for \(d=1\), the latent positions were significantly different. Is this a bug? Or how can we explain this?
Set up some metadata for this experiment¶
left_arange = np.arange(n_pairs)
right_arange = left_arange + n_pairs
embedding_1d_df = pd.DataFrame(index=np.arange(2 * n_pairs))
embedding_1d_df["pair_ind"] = np.concatenate((left_arange, left_arange))
embedding_1d_df["hemisphere"] = "Right"
embedding_1d_df.loc[left_arange, "hemisphere"] = "Left"
embedding_1d_df["x"] = 1
embedding_1d_df.loc[left_arange, "x"] = 0
Align and test the d=1, out embedding¶
Just like in the 2-sample testing above, we take the \(d=1\) embedding, align the left to the right, and ask whether these embeddings are different. Here I only use the out latent positions.
n_components = 1
op_left_out_latent, sp_left_out_latent = run_alignments(
left_out_latent[:, :n_components], right_out_latent[:, :n_components]
)
embedding_1d_df.loc[left_arange, "out_1d_align"] = op_left_out_latent[:, 0]
embedding_1d_df.loc[right_arange, "out_1d_align"] = right_out_latent[:, 0]
dcorr_results_1d_align = run_test(op_left_out_latent[:, :1], right_out_latent[:, :1])
ks_results_1d_align = ks_2samp(op_left_out_latent[:, 0], right_out_latent[:, 0])
print("DCorr 2-sample test on first out dimension, aligned in 1D:")
print(f"p-value = {dcorr_results_1d_align['pvalue']:0.4f}")
print("KS 2-sample test on first out dimension, aligned in 1D:")
print(f"p-value = {ks_results_1d_align[1]:0.4f}")
DCorr 2-sample test on first out dimension, aligned in 1D:
p-value = 0.0142
KS 2-sample test on first out dimension, aligned in 1D:
p-value = 0.0049
Align the \(d=8\) out embedding, test on the first dimension¶
Now, we instead perform the alignment in the \(d=8\) embedding. Then, we again look at only the first dimension of that aligned set of embeddings and test whether those are different.
n_components = 8
op_left_out_latent, sp_left_out_latent = run_alignments(
left_out_latent[:, :n_components], right_out_latent[:, :n_components]
)
embedding_1d_df.loc[left_arange, "out_8d_align"] = op_left_out_latent[:, 0]
embedding_1d_df.loc[right_arange, "out_8d_align"] = right_out_latent[:, 0]
dcorr_results_8d_align = run_test(op_left_out_latent[:, :1], right_out_latent[:, :1])
ks_results_8d_align = ks_2samp(op_left_out_latent[:, 0], right_out_latent[:, 0])
print("DCorr 2-sample test on first out dimension, aligned in 8D:")
print(f"p-value = {dcorr_results_8d_align['pvalue']:0.4f}")
print("KS 2-sample test on first out dimension, aligned in 8D:")
print(f"p-value = {ks_results_8d_align[1]:0.4f}")
DCorr 2-sample test on first out dimension, aligned in 8D:
p-value = 0.7249
KS 2-sample test on first out dimension, aligned in 8D:
p-value = 0.8575
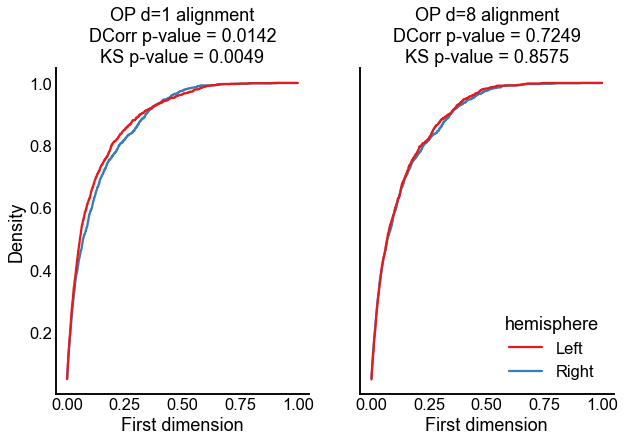
Plot the results for testing on the first dimension only¶
Below are empirical CDFs for the first dimension, in both of the cases described above. Note that in either case, the right embedding (blue line) is the same, because we aligned left to right.
fig, axs = plt.subplots(1, 2, figsize=(10, 6), sharey=True)
histplot_kws = dict(
stat="density",
cumulative=True,
element="poly",
common_norm=False,
bins=np.linspace(0, 1, 2000),
fill=False,
)
ax = axs[0]
sns.histplot(
data=embedding_1d_df,
x="out_1d_align",
ax=ax,
hue="hemisphere",
legend=False,
palette=palette,
**histplot_kws,
)
title = "OP d=1 alignment"
title += f"\nDCorr p-value = {dcorr_results_1d_align['pvalue']:0.4f}"
title += f"\nKS p-value = {ks_results_1d_align[1]:0.4f}"
ax.set(title=title, xlabel="First dimension")
ax = axs[1]
sns.histplot(
data=embedding_1d_df,
x="out_8d_align",
ax=ax,
hue="hemisphere",
palette=palette,
**histplot_kws,
)
title = "OP d=8 alignment"
title += f"\nDCorr p-value = {dcorr_results_8d_align['pvalue']:0.4f}"
title += f"\nKS p-value = {ks_results_8d_align[1]:0.4f}"
ax.set(title=title, xlabel="First dimension")
stashfig(
f"dim1-focus-cdf-test={test}-n_bootstraps={n_bootstraps}-preprocess={preprocess}"
)
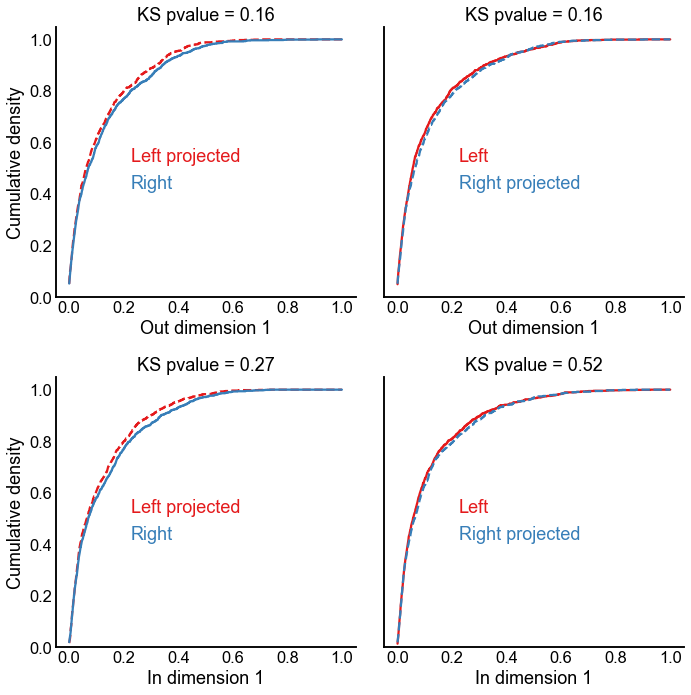
A projection experiment¶
Just to further put this issue of the first dimension to rest - here we look at what happens if we use the latent positions learned from the left to project the right-to-right adjacency matrix into the left latent space, and vice versa.
def get_projection_vector(v):
v = v.copy()
v /= np.linalg.norm(v) ** 2
return v
y_l = get_projection_vector(left_in_latent[:, 0])
y_r = get_projection_vector(right_in_latent[:, 0])
x_l = get_projection_vector(left_out_latent[:, 0])
x_r = get_projection_vector(right_out_latent[:, 0])
embedding_1d_df.loc[right_arange, "out_1d_proj"] = rr_adj @ y_l
embedding_1d_df.loc[left_arange, "out_1d_proj"] = ll_adj @ y_r
embedding_1d_df.loc[right_arange, "in_1d_proj"] = rr_adj.T @ x_l
embedding_1d_df.loc[left_arange, "in_1d_proj"] = ll_adj.T @ x_r
embedding_1d_df.loc[right_arange, "out_1d_proj_unscale"] = embedding_1d_df.loc[
right_arange, "out_1d_proj"
] / np.linalg.norm(embedding_1d_df.loc[right_arange, "out_1d_proj"])
embedding_1d_df.loc[left_arange, "out_1d_proj_unscale"] = embedding_1d_df.loc[
left_arange, "out_1d_proj"
] / np.linalg.norm(embedding_1d_df.loc[left_arange, "out_1d_proj"])
embedding_1d_df.loc[right_arange, "in_1d_proj_unscale"] = embedding_1d_df.loc[
right_arange, "in_1d_proj"
] / np.linalg.norm(embedding_1d_df.loc[right_arange, "in_1d_proj"])
embedding_1d_df.loc[left_arange, "in_1d_proj_unscale"] = embedding_1d_df.loc[
left_arange, "in_1d_proj"
] / np.linalg.norm(embedding_1d_df.loc[left_arange, "in_1d_proj"])
embedding_1d_df.loc[right_arange, "out_1d"] = right_out_latent[:, 0]
embedding_1d_df.loc[left_arange, "out_1d"] = left_out_latent[:, 0]
embedding_1d_df.loc[right_arange, "in_1d"] = right_in_latent[:, 0]
embedding_1d_df.loc[left_arange, "in_1d"] = left_in_latent[:, 0]
embedding_1d_df.loc[right_arange, "out_1d_unscale"] = right_out_latent[
:, 0
] / np.linalg.norm(right_out_latent[:, 0])
embedding_1d_df.loc[left_arange, "out_1d_unscale"] = left_out_latent[
:, 0
] / np.linalg.norm(left_out_latent[:, 0])
embedding_1d_df.loc[right_arange, "in_1d_unscale"] = right_in_latent[
:, 0
] / np.linalg.norm(right_in_latent[:, 0])
embedding_1d_df.loc[left_arange, "in_1d_unscale"] = left_in_latent[
:, 0
] / np.linalg.norm(left_in_latent[:, 0])
histplot_kws = dict(
palette=palette,
hue="hemisphere",
legend=False,
stat="density",
cumulative=True,
element="poly",
common_norm=False,
bins=np.linspace(0, 1, 2000),
fill=False,
)
def plot_dimension(proj, in_out, ax, unscale=False):
left_text = "Left"
right_text = "Right"
if proj == "Left":
x_left = f"{in_out}_1d_proj"
x_right = f"{in_out}_1d"
left_linestyle = "--"
right_linestyle = "-"
left_text += " projected"
else:
x_right = f"{in_out}_1d_proj"
x_left = f"{in_out}_1d"
left_linestyle = "-"
right_linestyle = "--"
right_text += " projected"
left_df = embedding_1d_df[embedding_1d_df["hemisphere"] == "Left"]
right_df = embedding_1d_df[embedding_1d_df["hemisphere"] == "Right"]
if unscale:
x_left = x_left + "_unscale"
x_right = x_right + "_unscale"
sns.histplot(
data=left_df,
x=x_left,
ax=ax,
linestyle=left_linestyle,
**histplot_kws,
)
sns.histplot(
data=right_df,
x=x_right,
ax=ax,
linestyle=right_linestyle,
**histplot_kws,
)
ax.text(0.25, 0.5, left_text, color=palette["Left"], transform=ax.transAxes)
ax.text(0.25, 0.4, right_text, color=palette["Right"], transform=ax.transAxes)
left_data = left_df[x_left].values
right_data = right_df[x_right].values
stat, pvalue = ks_2samp(left_data, right_data)
ax.set(title=f"KS pvalue = {pvalue:0.2f}", ylabel="Cumulative density")
if in_out == "in":
ax.set_xlabel("In dimension 1")
else:
ax.set_xlabel("Out dimension 1")
fig, axs = plt.subplots(2, 2, figsize=(10, 10), sharey=True)
plot_dimension("Left", "out", axs[0, 0])
plot_dimension("Right", "out", axs[0, 1])
plot_dimension("Left", "in", axs[1, 0])
plot_dimension("Right", "in", axs[1, 1])
plt.tight_layout()
stashfig("projection-1d-comparison")
Double check that the identical pvalues are real¶
x_left = "out_1d_proj"
x_right = "out_1d"
left_data = embedding_1d_df[embedding_1d_df["hemisphere"] == "Left"][x_left].values
right_data = embedding_1d_df[embedding_1d_df["hemisphere"] == "Right"][x_right].values
print("Epps-Singleton 2-sample on left projected vs. right first out dimension:")
print(f"p-value = {epps_singleton_2samp(left_data, right_data)[1]}")
print()
x_left = "out_1d"
x_right = "out_1d_proj"
left_data = embedding_1d_df[embedding_1d_df["hemisphere"] == "Left"][x_left].values
right_data = embedding_1d_df[embedding_1d_df["hemisphere"] == "Right"][x_right].values
print("Epps-Singleton 2-sample on left vs. right projected first out dimension:")
print(f"p-value = {epps_singleton_2samp(left_data, right_data)[1]}")
Epps-Singleton 2-sample on left projected vs. right first out dimension:
p-value = 0.1622046313983571
Epps-Singleton 2-sample on left vs. right projected first out dimension:
p-value = 0.6116909673886892
Run the projection experiment but without singular value scaling¶
fig, axs = plt.subplots(2, 2, figsize=(10, 10), sharey=True)
histplot_kws["bins"] = np.linspace(0, 0.2, 2000)
plot_dimension("Left", "out", axs[0, 0], unscale=True)
plot_dimension("Right", "out", axs[0, 1], unscale=True)
plot_dimension("Left", "in", axs[1, 0], unscale=True)
plot_dimension("Right", "in", axs[1, 1], unscale=True)
plt.tight_layout()
stashfig("projection-1d-comparison-unscaled")
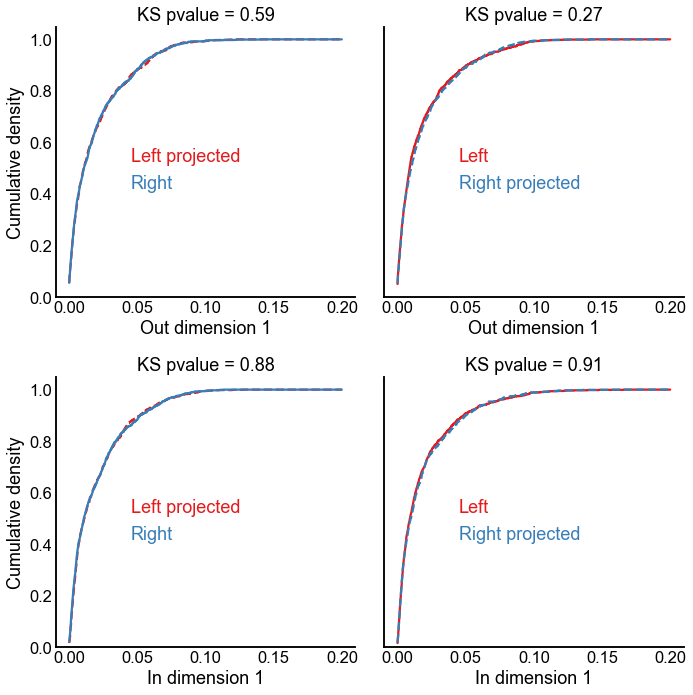
Test the 2-dimensional joint distributions¶
scatter_kws = dict(hue="hemisphere", palette=palette, s=10, linewidth=0, alpha=0.5)
def plot_paired_dimension(proj, ax, unscale=False):
left_text = "Left"
right_text = "Right"
x_left = "out_1d"
y_left = "in_1d"
x_right = "out_1d"
y_right = "in_1d"
if proj == "Left":
x_left += "_proj"
y_left += "_proj"
left_text += " projected"
else:
x_right += "_proj"
y_right += "_proj"
right_text += " projected"
if unscale:
x_left += "_unscale"
x_right += "_unscale"
y_left += "_unscale"
y_right += "_unscale"
left_df = embedding_1d_df[embedding_1d_df["hemisphere"] == "Left"]
right_df = embedding_1d_df[embedding_1d_df["hemisphere"] == "Right"]
sns.scatterplot(data=left_df, x=x_left, y=y_left, ax=ax, **scatter_kws)
sns.scatterplot(data=right_df, x=x_right, y=y_right, ax=ax, **scatter_kws)
ax.get_legend().remove()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
maxlim = max(xlim[1], ylim[1])
minlim = min(xlim[0], ylim[0])
xlim = (minlim, maxlim)
ylim = (minlim, maxlim)
ax.set(xlabel="Out dimension 1", ylabel="In dimension 1", ylim=ylim, xlim=xlim)
ax.text(0.65, 0.95, left_text, color=palette["Left"], transform=ax.transAxes)
ax.text(0.65, 0.88, right_text, color=palette["Right"], transform=ax.transAxes)
left_data = left_df[[x_left, y_left]].values
right_data = right_df[[x_right, y_right]].values
test_results = run_test(left_data, right_data)
pvalue = test_results["pvalue"]
ax.set_title(f"DCorr 2S p-value = {pvalue:.3g}")
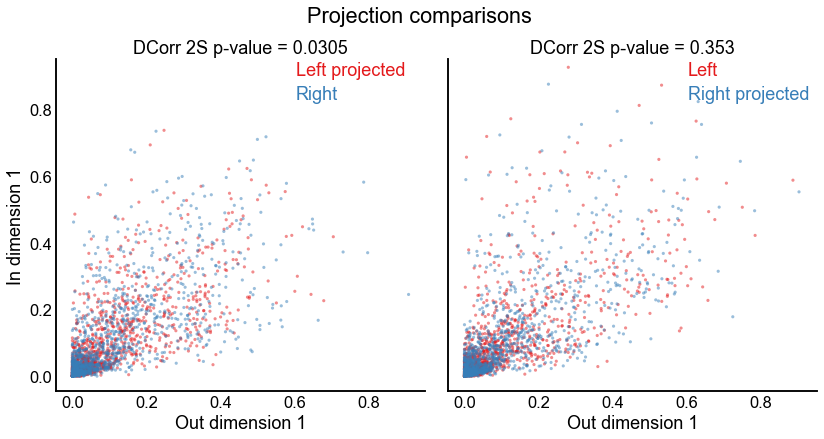
fig, axs = plt.subplots(1, 2, figsize=(12, 6), sharex=True, sharey=True)
plot_paired_dimension("Left", axs[0], unscale=False)
plot_paired_dimension("Right", axs[1], unscale=False)
plt.tight_layout()
fig.suptitle("Projection comparisons", y=1.03)
stashfig("projection-2d-comparison")
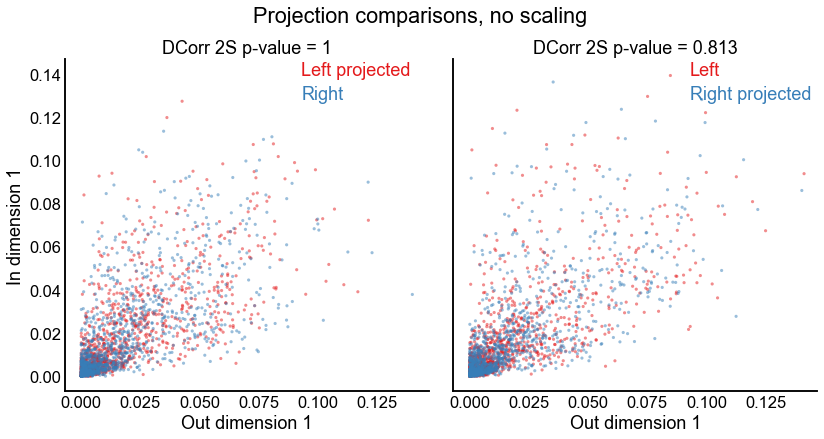
Test the 2-dimensional joints but without singular value scaling¶
fig, axs = plt.subplots(1, 2, figsize=(12, 6), sharex=True, sharey=True)
plot_paired_dimension("Left", axs[0], unscale=True)
plot_paired_dimension("Right", axs[1], unscale=True)
plt.tight_layout()
fig.suptitle("Projection comparisons, no scaling", y=1.03)
stashfig("projection-2d-comparison-unscaled")
A “corrected” version of this test¶
We saw above that the alignment makes a huge difference in the outcome of the test. One possible way to fix this is to use a higher embedding dimension where the alignment is good, and then perform our test for varying numbers of kept dimensions (just like we did above where we aligned in \(d=8\) and tested the first \(d=1\) dimensions).
In this case, I use \(d=12\) as the alignment dimension, and test for \(d=1\), \(d=2\) etc. Note that testing at \(d=2\) means testing on the first 2 dimensions, not the second dimension alone.
align_n_components = (
12 # this is one of the dimensions where we failed to reject before
)
op_left_out_latent, sp_left_out_latent = run_alignments(
left_out_latent[:, :align_n_components], right_out_latent[:, :align_n_components]
)
op_left_in_latent, sp_left_in_latent = run_alignments(
left_in_latent[:, :align_n_components], right_in_latent[:, :align_n_components]
)
rows = []
for n_components in np.arange(1, align_n_components + 1):
left_out = op_left_out_latent.copy()[:, :n_components]
left_in = op_left_in_latent.copy()[:, :n_components]
right_out = right_out_latent[:, :align_n_components].copy()[:, :n_components]
right_in = right_in_latent[:, :align_n_components].copy()[:, :n_components]
left_composite_latent = np.concatenate((left_out, left_in), axis=1)
right_composite_latent = np.concatenate((right_out, right_in), axis=1)
run_test(
left_composite_latent,
right_composite_latent,
rows,
info={"alignment": "OP", "n_components": n_components},
)
left_out = sp_left_out_latent.copy()[:, :n_components]
left_in = sp_left_in_latent.copy()[:, :n_components]
left_composite_latent = np.concatenate((left_out, left_in), axis=1)
run_test(
left_composite_latent,
right_composite_latent,
rows,
info={"alignment": "O-SP", "n_components": n_components},
)
corrected_results = pd.DataFrame(rows)
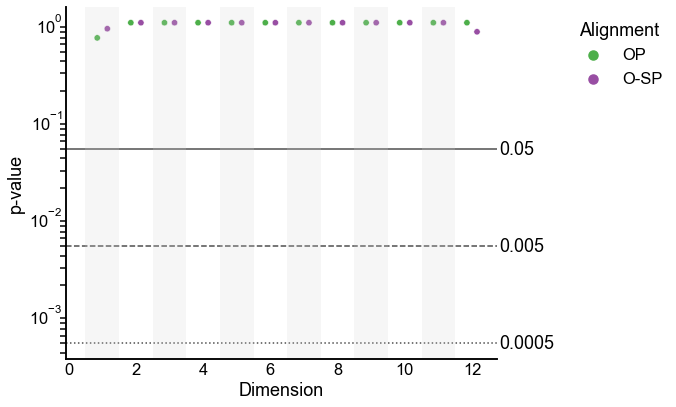
Plot the results of the corrected version which starts from a good alignment¶
Here I plot the results only for orthogonal Procrustes. The behavior of the p-values is much closer to what we would have expected.
plot_pvalues(corrected_results)
End¶
elapsed = time.time() - t0
delta = datetime.timedelta(seconds=elapsed)
print("----")
print(f"Script took {delta}")
print(f"Completed at {datetime.datetime.now()}")
print("----")
----
Script took 0:14:32.475558
Completed at 2021-03-15 11:13:34.544446
----
