Test for bilateral symmetry - latent distribution test¶
Preliminaries¶
from pkg.utils import set_warnings
import datetime
import pprint
import time
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from giskard.utils import get_paired_inds
from graspologic.align import OrthogonalProcrustes, SeedlessProcrustes
from graspologic.embed import AdjacencySpectralEmbed, select_dimension
from graspologic.utils import (
augment_diagonal,
binarize,
pass_to_ranks,
)
from hyppo.ksample import KSample
from pkg.data import (
load_maggot_graph,
load_network_palette,
load_node_palette,
select_nice_nodes,
)
from pkg.io import savefig
from pkg.plot import set_theme
from giskard.align import joint_procrustes
def stashfig(name, **kwargs):
foldername = "latent_distribution_test"
savefig(name, foldername=foldername, **kwargs)
Load and process data¶
t0 = time.time()
set_theme()
network_palette, NETWORK_KEY = load_network_palette()
node_palette, NODE_KEY = load_node_palette()
mg = load_maggot_graph()
mg = select_nice_nodes(mg)
nodes = mg.nodes
left_nodes = nodes[nodes["hemisphere"] == "L"]
left_inds = left_nodes["_inds"]
right_nodes = nodes[nodes["hemisphere"] == "R"]
right_inds = right_nodes["_inds"]
left_paired_inds, right_paired_inds = get_paired_inds(
nodes, pair_key="predicted_pair", pair_id_key="predicted_pair_id"
)
right_paired_inds_shifted = right_paired_inds - len(left_inds)
adj = mg.sum.adj
ll_adj = adj[np.ix_(left_inds, left_inds)]
rr_adj = adj[np.ix_(right_inds, right_inds)]
Removed 13 nodes when taking the largest connected component.
Removed 38 nodes when removing pendants.
Removed 0 nodes when taking the largest connected component.
Embed the network using adjacency spectral embedding¶
def preprocess_for_embed(ll_adj, rr_adj, preprocess):
if "binarize" in preprocess:
ll_adj_to_embed = binarize(ll_adj)
rr_adj_to_embed = binarize(rr_adj)
if "rescale" in preprocess:
ll_norm = np.linalg.norm(ll_adj_to_embed, ord="fro")
rr_norm = np.linalg.norm(rr_adj_to_embed, ord="fro")
mean_norm = (ll_norm + rr_norm) / 2
ll_adj_to_embed *= mean_norm / ll_norm
rr_adj_to_embed *= mean_norm / rr_norm
return ll_adj_to_embed, rr_adj_to_embed
def embed(adj, n_components=40, ptr=False):
if ptr:
adj = pass_to_ranks(adj)
elbow_inds, _ = select_dimension(augment_diagonal(adj), n_elbows=5)
elbow_inds = np.array(elbow_inds)
ase = AdjacencySpectralEmbed(n_components=n_components)
out_latent, in_latent = ase.fit_transform(adj)
return out_latent, in_latent, ase.singular_values_, elbow_inds
def split_adj(adj):
ll_adj = adj[np.ix_(left_inds, left_inds)]
rr_adj = adj[np.ix_(right_inds, right_inds)]
lr_adj = adj[np.ix_(left_inds, right_inds)]
rl_adj = adj[np.ix_(right_inds, left_inds)]
return ll_adj, rr_adj, lr_adj, rl_adj
align_n_components = 24
preprocess = ["binarize", "rescale"]
raw_adj = mg.sum.adj.copy()
ll_adj, rr_adj, _, _ = split_adj(raw_adj)
ll_adj_to_embed, rr_adj_to_embed = preprocess_for_embed(ll_adj, rr_adj, preprocess)
X_ll, Y_ll, left_sing_vals, left_elbow_inds = embed(
ll_adj_to_embed, n_components=align_n_components
)
X_rr, Y_rr, right_sing_vals, right_elbow_inds = embed(
rr_adj_to_embed, n_components=align_n_components
)
/Users/bpedigo/JHU_code/maggot/graspologic/graspologic/embed/ase.py:166: UserWarning: Input graph is not fully connected. Results may notbe optimal. You can compute the largest connected component byusing ``graspologic.utils.largest_connected_component``.
warnings.warn(msg, UserWarning)
X_ll, Y_ll = joint_procrustes(
(X_ll, Y_ll),
(X_rr, Y_rr),
method="seeded",
seeds=(left_paired_inds, right_paired_inds_shifted),
)
Hypothesis testing on the embeddings¶
To test whether the distribution of latent positions is different, we use the approach of the “nonpar” test, also called the latent distribution test. Here, for the backend 2-sample test, we use distance correlation (Dcorr).
test = "dcorr"
workers = -1
auto = True
if auto:
n_bootstraps = None
else:
n_bootstraps = 500
def run_test(
X1,
X2,
rows=None,
info={},
auto=auto,
n_bootstraps=n_bootstraps,
workers=workers,
test=test,
print_out=False,
):
currtime = time.time()
test_obj = KSample(test)
tstat, pvalue = test_obj.test(
X1,
X2,
reps=n_bootstraps,
workers=workers,
auto=auto,
)
elapsed = time.time() - currtime
row = {
"pvalue": pvalue,
"tstat": tstat,
"elapsed": elapsed,
}
row.update(info)
if print_out:
pprint.pprint(row)
if rows is not None:
rows.append(row)
else:
return row
Run the two-sample test for varying embedding dimension¶
rows = []
for n_components in np.arange(1, align_n_components + 1):
left_composite_latent = np.concatenate(
(X_ll[:, :n_components], Y_ll[:, :n_components]), axis=1
)
right_composite_latent = np.concatenate(
(X_rr[:, :n_components], Y_rr[:, :n_components]), axis=1
)
run_test(
left_composite_latent,
right_composite_latent,
rows,
info={"alignment": "SOP", "n_components": n_components},
)
results = pd.DataFrame(rows)
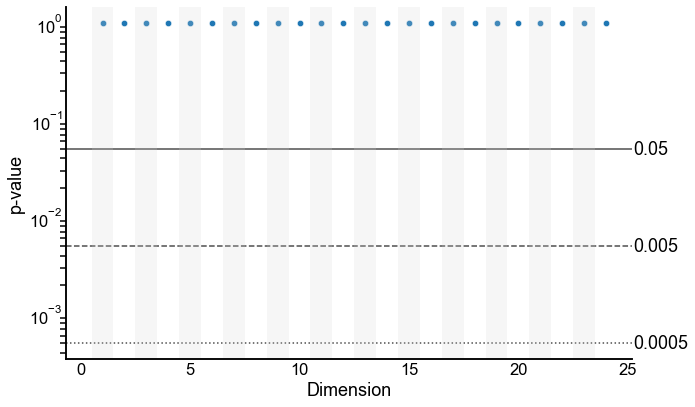
Plot the 2-sample test p-values by varying dimension¶
Note: these are on a log y-scale.
def plot_pvalues(results, line_locs=[0.05, 0.005, 0.0005]):
results = results.copy()
styles = ["-", "--", ":"]
line_kws = dict(color="black", alpha=0.7, linewidth=1.5, zorder=-1)
# plot p-values by embedding dimension
_, ax = plt.subplots(1, 1, figsize=(10, 6))
sns.scatterplot(
data=results,
x="n_components",
y="pvalue",
ax=ax,
s=40,
)
ax.set_yscale("log")
styles = ["-", "--", ":"]
line_kws = dict(color="black", alpha=0.7, linewidth=1.5, zorder=-1)
for loc, style in zip(line_locs, styles):
ax.axhline(loc, linestyle=style, **line_kws)
ax.text(ax.get_xlim()[-1] + 0.1, loc, loc, ha="left", va="center")
ax.set(xlabel="Dimension", ylabel="p-value")
# ax.get_legend().remove()
# ax.legend(bbox_to_anchor=(1.15, 1), loc="upper left", title="Alignment")
xlim = ax.get_xlim()
for x in range(1, int(xlim[1]), 2):
ax.axvspan(x - 0.5, x + 0.5, color="lightgrey", alpha=0.2, linewidth=0)
plt.tight_layout()
plot_pvalues(results)
stashfig(
f"naive-pvalues-test={test}-n_bootstraps={n_bootstraps}-preprocess={preprocess}"
)
Now do a synthetic alternative experiment¶
from sklearn.preprocessing import normalize
align_n_components = 16
n_perturb = 10
do_normalize = True
groups = ["None", "MBONs", "MBINs", "PNs", "KCs", "sensories", "LNs"]
rows = []
for group in groups:
print(group)
ll_adj_perturbed = ll_adj_to_embed.copy()
if group != "None":
group_nodes = left_nodes[left_nodes["simple_group"] == group]
effective_n_perturb = min(n_perturb, len(group_nodes))
perturb_index = np.random.choice(
group_nodes.index, size=effective_n_perturb, replace=False
)
perturb_inds = group_nodes.loc[perturb_index, "_inds"]
for i in perturb_inds:
perm_inds = np.random.permutation(len(ll_adj))
ll_adj_perturbed[i] = ll_adj_perturbed[i, perm_inds]
perm_inds = np.random.permutation(len(ll_adj))
ll_adj_perturbed[:, i] = ll_adj_perturbed[perm_inds, i]
else:
effective_n_perturb = 0
X_ll, Y_ll, left_sing_vals, left_elbow_inds = embed(
ll_adj_perturbed, n_components=align_n_components
)
X_rr, Y_rr, right_sing_vals, right_elbow_inds = embed(
rr_adj_to_embed, n_components=align_n_components
)
if do_normalize:
X_ll = normalize(X_ll)
Y_ll = normalize(Y_ll)
X_rr = normalize(X_rr)
Y_rr = normalize(Y_rr)
X_ll, Y_ll = joint_procrustes(
(X_ll, Y_ll),
(X_rr, Y_rr),
method="seeded",
seeds=(left_paired_inds, right_paired_inds_shifted),
)
for n_components in np.arange(1, align_n_components + 1):
left_composite_latent = np.concatenate(
(X_ll[:, :n_components], Y_ll[:, :n_components]), axis=1
)
# left_composite_latent = normalize(left_composite_latent)
right_composite_latent = np.concatenate(
(X_rr[:, :n_components], Y_rr[:, :n_components]), axis=1
)
# right_composite_latent = normalize(right_composite_latent)
run_test(
left_composite_latent,
right_composite_latent,
rows,
info={
"alignment": "SOP",
"n_components": n_components,
"perturb_group": group,
"n_perturb": effective_n_perturb,
},
)
results = pd.DataFrame(rows)
results
None
/Users/bpedigo/JHU_code/maggot/graspologic/graspologic/embed/ase.py:166: UserWarning: Input graph is not fully connected. Results may notbe optimal. You can compute the largest connected component byusing ``graspologic.utils.largest_connected_component``.
warnings.warn(msg, UserWarning)
MBONs
/Users/bpedigo/JHU_code/maggot/graspologic/graspologic/embed/ase.py:166: UserWarning: Input graph is not fully connected. Results may notbe optimal. You can compute the largest connected component byusing ``graspologic.utils.largest_connected_component``.
warnings.warn(msg, UserWarning)
MBINs
/Users/bpedigo/JHU_code/maggot/graspologic/graspologic/embed/ase.py:166: UserWarning: Input graph is not fully connected. Results may notbe optimal. You can compute the largest connected component byusing ``graspologic.utils.largest_connected_component``.
warnings.warn(msg, UserWarning)
PNs
/Users/bpedigo/JHU_code/maggot/graspologic/graspologic/embed/ase.py:166: UserWarning: Input graph is not fully connected. Results may notbe optimal. You can compute the largest connected component byusing ``graspologic.utils.largest_connected_component``.
warnings.warn(msg, UserWarning)
KCs
/Users/bpedigo/JHU_code/maggot/graspologic/graspologic/embed/ase.py:166: UserWarning: Input graph is not fully connected. Results may notbe optimal. You can compute the largest connected component byusing ``graspologic.utils.largest_connected_component``.
warnings.warn(msg, UserWarning)
sensories
/Users/bpedigo/JHU_code/maggot/graspologic/graspologic/embed/ase.py:166: UserWarning: Input graph is not fully connected. Results may notbe optimal. You can compute the largest connected component byusing ``graspologic.utils.largest_connected_component``.
warnings.warn(msg, UserWarning)
LNs
/Users/bpedigo/JHU_code/maggot/graspologic/graspologic/embed/ase.py:166: UserWarning: Input graph is not fully connected. Results may notbe optimal. You can compute the largest connected component byusing ``graspologic.utils.largest_connected_component``.
warnings.warn(msg, UserWarning)
| pvalue | tstat | elapsed | alignment | n_components | perturb_group | n_perturb | |
|---|---|---|---|---|---|---|---|
| 0 | 0.606708 | -0.000248 | 0.899064 | SOP | 1 | None | 0 |
| 1 | 1.000000 | -0.000479 | 0.783196 | SOP | 2 | None | 0 |
| 2 | 1.000000 | -0.000662 | 0.797197 | SOP | 3 | None | 0 |
| 3 | 1.000000 | -0.000716 | 0.828584 | SOP | 4 | None | 0 |
| 4 | 1.000000 | -0.000573 | 0.784464 | SOP | 5 | None | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 107 | 0.002860 | 0.002664 | 0.759584 | SOP | 12 | LNs | 10 |
| 108 | 0.003563 | 0.002529 | 0.769080 | SOP | 13 | LNs | 10 |
| 109 | 0.000889 | 0.003391 | 0.767693 | SOP | 14 | LNs | 10 |
| 110 | 0.000226 | 0.004253 | 0.767576 | SOP | 15 | LNs | 10 |
| 111 | 0.000408 | 0.003880 | 0.776073 | SOP | 16 | LNs | 10 |
112 rows × 7 columns
node_palette["None"] = "#808080" # grey
n_perturbs = results.groupby("perturb_group")["n_perturb"].first()
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
sns.lineplot(
data=results,
x="n_components",
y="pvalue",
hue="perturb_group",
palette=node_palette,
)
ax.set_yscale("log")
handles, labels = ax.get_legend_handles_labels()
new_labels = []
for label in labels:
new_labels.append(label + f" ({n_perturbs[label]})")
ax.get_legend().remove()
ax.legend(
handles=handles,
labels=new_labels,
bbox_to_anchor=(1.15, 1),
loc="upper left",
title="Perturb\ngroup",
)
styles = ["-", "--", ":"]
line_locs = [0.05, 0.005, 0.0005]
line_kws = dict(color="black", alpha=0.7, linewidth=1.5, zorder=-1)
for loc, style in zip(line_locs, styles):
ax.axhline(loc, linestyle=style, **line_kws)
ax.text(ax.get_xlim()[-1] + 0.1, loc, loc, ha="left", va="center")
ax.set(xlabel="# of dimensions", ylabel='p-value')
stashfig(
f"perturb-p-values-n_perturb={n_perturb}-align_n_component={align_n_components}-normalize={do_normalize}"
)
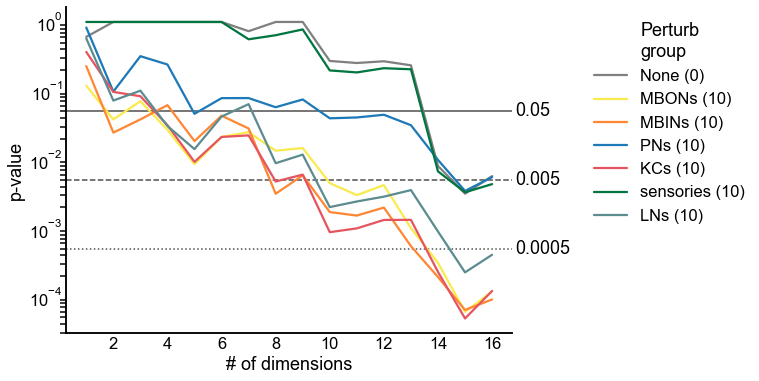
End¶
elapsed = time.time() - t0
delta = datetime.timedelta(seconds=elapsed)
print("----")
print(f"Script took {delta}")
print(f"Completed at {datetime.datetime.now()}")
print("----")
----
Script took 0:05:07.648001
Completed at 2021-05-13 11:19:00.387545
----
