Learning Network Representations
5. Learning Network Representations#
As you know by now, network-valued data has many properties that differentiate it from more traditional representations of data. The benefit, in this case, is that networks have a particular topological structure: the manner in which the edges and nodes manifest gives useful information about relationships between the nodes, and not just about each node individually. However, this structure comes with a drawback: the vast majority of machine learning, to date, is designed for tabular (or, multivariate) structures, in which each observation you have tends to be treated independently (or more generally, prescribably dependently) from the other observations you make. What we mean by prescribably dependently is that the observations of data might not be totally independent, but the dependencies can, at the very least, be reasonably modelled in such a way that inference is possible.
In network-valued data, with \(n\) nodes, there are \(n!\) possible dependencies that could exist in the data (that is, each node could be dependent on the other nodes, which in turn are dependent on other nodes, so on and so forth, for all of the nodes in the network). To make this a bit more tractable to learn from, in network learning, we will tend to serialize the network using one of the representations which you learned about in Section 3.3. For network learning, the most common approach that we will use is the Section 3.3.3 approach, in which you will learn a useful representation for each node. There are a variety of ways which you will use to do this, the most common of which tend to be various types of spectral embeddings. When you see multiple networks, you will learn representations which are a combination of the Section 3.3.3 and Section 3.3.4, in which each you will learn a representation of each node for each network. This chapter fits in somewhere around here in the useful figure we’ve been working up along the way:
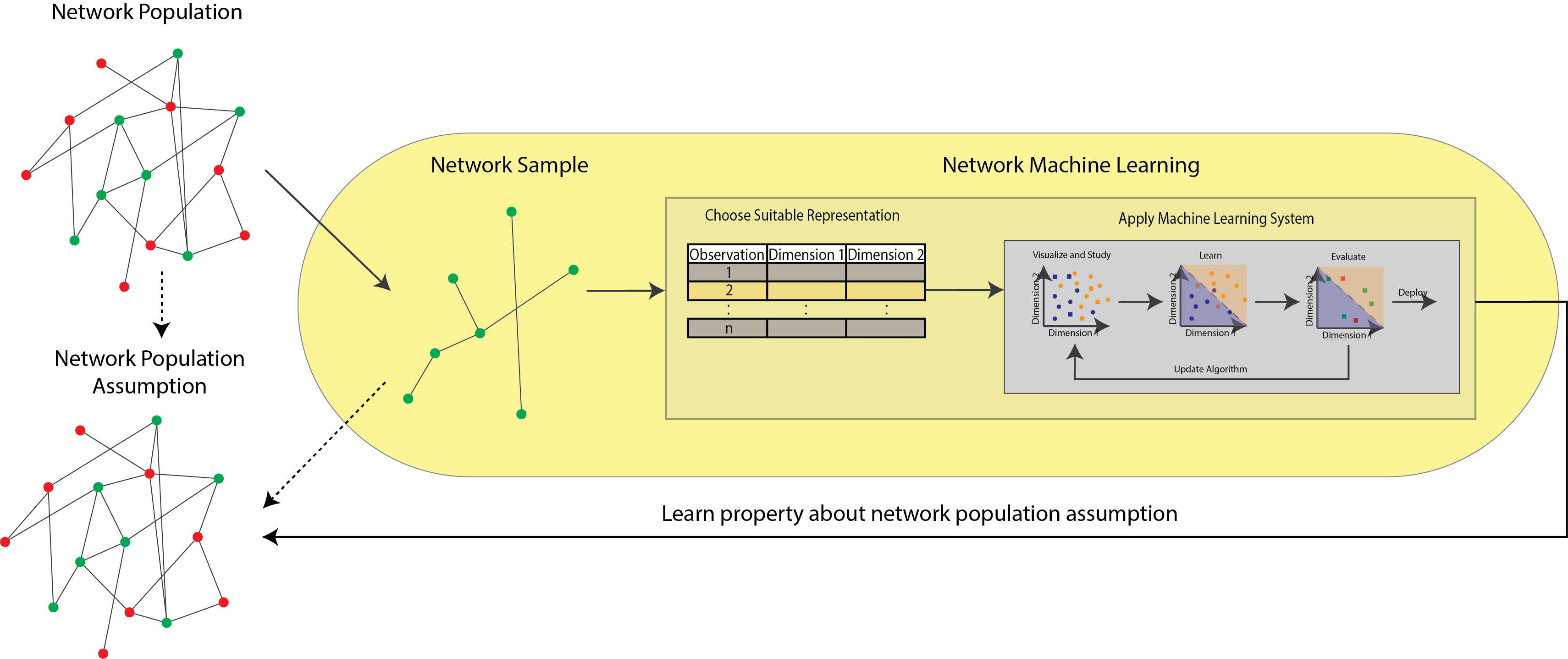
Fig. 5.1 The statistical learning pipeline. In this chapter, you will learn about how to represent networks you observe in your analysis.#
It is important to note that to learn and derive useful insights from these representations, you really don’t need to understand anything about the last chapter at all, in general. You can take the representations you learn about, apply machine learning systems to them, and then study the networks in isolation. However, these representations tend to make more intuitive sense in the context of Section 4, and further, Section 4 provides context and assumptions in which these representations directly motivate many of the applications you will learn in Section 7 onwards. So, we’d recommend learning this chapter somewhat in tandem with the preceding section: as you learn a new algorithm for finding a representation of a network, go back and think about how that representation is motivated by a statistical model in the preceding section. This will help you as you get to the later chapters understand how the pieces start to fit together in the Network Machine Learning landscape. We have the following sections:
Having a complete understanding of the results in this section, and particularly, the justification for why we approach network representation problems in the way in which we do requires some comprehensive mathematical background. For this reason, we have prepared the supplementary section Section 12 for more advanced readers.

