1.4. Challenges of Network Machine Learning

Like other branches of science, network machine learning is not without its challenges. While we don’t expect you to be versed in network science just yet, we’ll try to explore some of the issues here.

1.4.1. Acquiring the network

Obtaining observations of networks can be difficult or expensive. For some applications, such as social media, it is simply a matter of pushing numbers through the right API, such as pulling the users in the network and their friends lists, and cross-referencing who in the network is friends with who to put together edges. In many other domains of science, we don’t have this elegant method. In electron microscopy connectomics, networks are acquired after a lengthy data acquisition and pre-processing procedure. To start, the organisms must be cultivated to answer a scientific question, such as developing a large collection of the particular phenotype (scientific word for, the specific characteristic) you want to study. These organisms then need to have their nervous systems excluded and prepared via microscope slides, which requires tools which can reliably cut biological tissue with near perfect precision as small as tens of microns (a human hair is about 100 microns thick). This has to be repeated over the entire nervous system of the organism, and then imaged with expensive devices called electron microscopes. Next, the individual slides (of which there are often millions per organism) have to be reconstructed digitally, and segmented to identify the individual neurons in the brain. Finally, expensive processing techniques take these neurons, and trace out the paths of the neuron which connect to other neurons to put together a map of the brain. This whole process costs a lot of money, time, and effort to be able to do reliably and repeatably just to be able to obtain a network in the first place.

1.4.2. What is statistical network machine learning?

In this book on network machine learning, we are going to focus some level of attention on a particular sub-branch of machine learning, known as statistical learning. Statistical learning is a framework for machine learning in which we infer things about our network, we use statitistics to refine and conceptualize our problem and quantify how reasonable our conclusions are. What exactly do we mean by this?

1.4.2.1. We might errorfully observe the networks

Finally, any network you might observe might be somewhat random. Let’s say in the case of the social network, that people connect with others that simply are recommended by the social network to them. You could try to exhaustively understand why the network showed them the person, and maybe come up with a deterministic strategy that determines perfectly who is connected to who, but this might represent learning extremely personal, and identifying, information about the people that the social network does not make accessible to scientists. Further, the networks might not necessarily be deterministic. There might be errors in how the network is observed, in that some connections might exist in the data that don’t exist in reality, or vice versa. In Fig. 1.12, we see an example of an errorfully observed network sample.

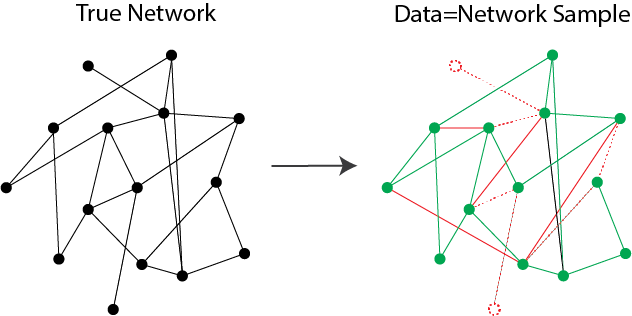
Fig. 1.12 The true underlying network contains a lot of information that in the course of observing or sampling the network, we don’t actually measure properly. In the left, we see the network which underlies the sample we obtain. In the sample, we might not see some of the nodes (red dashed nodes), we might not see some of the edges (red dashed edges), or we might see edges which shouldn’t really be present (red solid edges). While a portion of the network might faithfully represent the underlying system (green nodes and edges), we don’t actually get to see what part of our sample is faithful or unfaithful with respect to the underlying network.

1.4.2.2. We might not see the whole network

When we study a network, it is rare that we observe the entire system perfectly in its entirety. Consider, for instance, the case of a social network, in which the nodes of our network are people within the network, and edges are whether groups of people are friends with one another in the social network. In this instance, we could approach the problem in one of two ways. On one hand, we could collect our data for literally every single person in the network. We could study a network with millions or hundreds of millions of nodes, and with an equally (if not even larger) collection of edges representing whether these people are friends. In Fig. 1.13, we look at an example where we don’t get to see all the nodes of the network.

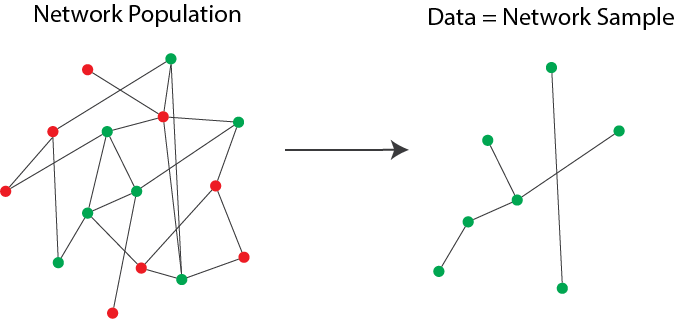
Fig. 1.13 The true underlying network has both green and red nodes, indicated in the left panel. However, when we sample the network on the right, our sample only includes the subset of nodes that are green.

1.4.2.3. We might only see a subset of the networks

On a related note, let’s imagine that we have a brain network. In this brain network, we have several areas of the brain responsible for different function: we have areas of the brain that are responsible for different aspects of eyesight, different aspects of movement, and many other physical or mental functions. In this example, our edges will be whether two brain areas can communicate with one another. By communicate, we mean that the brain area can inform processes that are performed elsewhere in the brain. For instance, if you decide to move your arm to grab a soda, some of the brain areas responsible for eyesight might need to communicate with some of the brain areas responsible for movement. A psychologist hypothesizes that for an individual who is a musician, some of these brain connections might be stronger, in that they might be more or less likely to occur in an individual who is a musician than an individual who is not a musician. He could collect data in the form of brain networks for every single individual who is or is not a musician, and directly study whether some of the brain areas have different levels of communication in the group of people who are musicians compared to those who are not without needing statistics at all. In Fig. 1.14, we see an example where we only get to sample a subset of the networks in the underlying population. This is more common than the alternative; there are a lot of people on earth the psychologist would need to study to be able to make his claim without doing any statistics!

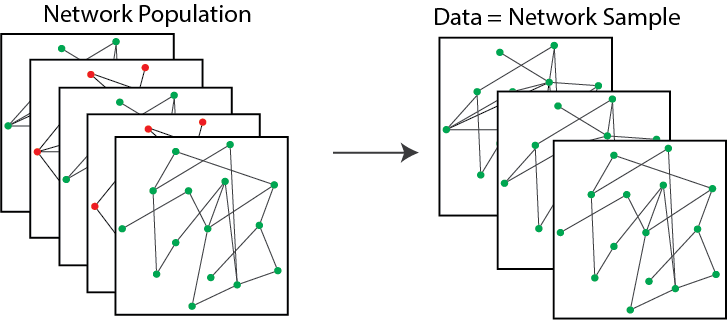
Fig. 1.14 The true underlying population contains many more networks than we are able to actually sample. In the left panel, we have green and red networks, but in the sample, we only get to see the red networks.

1.4.2.4. We can never collect perfect data nor see everything

In all of these simple examples, there is a big problem: obtaining the data necessary to answer the question is simply infeasible. There are infinitely many ways in which small deviations in your network, or networks, that you actually get to analyze might have imperfections which can most efficiently be described as random. The collection of all of the possible data that could be obtained for an experiment is what is referred to as the population. While one expert might focus all of his attention on obtaining the entire network they hope to study, a more diligent expert might use another strategy. Rather than collecting data from every single person on the social network, or obtaining brain networks from every single person who could potentially be a musician, or collecting pristine data that always represents the underlying network perfectly, you might instead just look at a reasonably sized subset of data which you can feasibly obtain. Maybe this means collecting your social network with only \(1000\) nodes instead of one hundred million, or maybe this means looking at \(200\) networks instead of brain networks from every person in the United States. Or, this might mean using the network sample you have, and simply accepting that it doesn’t perfectly represent the underlying system.

1.4.2.5. Statistics allows us to bridge what we learn from what we see with what we didn’t get to see

In these cases, what you have done is you have collected a sample, which can be loosely defined as a set of objects which is collected from the population in some way. The sample itself is where statistics comes into play. The reason this is critical is that, when you reach a conclusion, you do not want to reach a conclusion that only applies to the specific group of people, or the specific network, that you analyzed in your sample. Statistics allows you to be as specific as you can about how, exactly, conclusions that you reach on the sample apply to the general population. We try to summarize the relationship in Fig. 1.15. Throughout this book, the sample itself, and how it relates to the underlying population, will always be in focus and should be at the forefront of your mind. When we get to the sections on statistical learning in Section 3, we’ll rotate back to our discussion on statistical learning, and provide a more rigorous definition than we’ve given here.

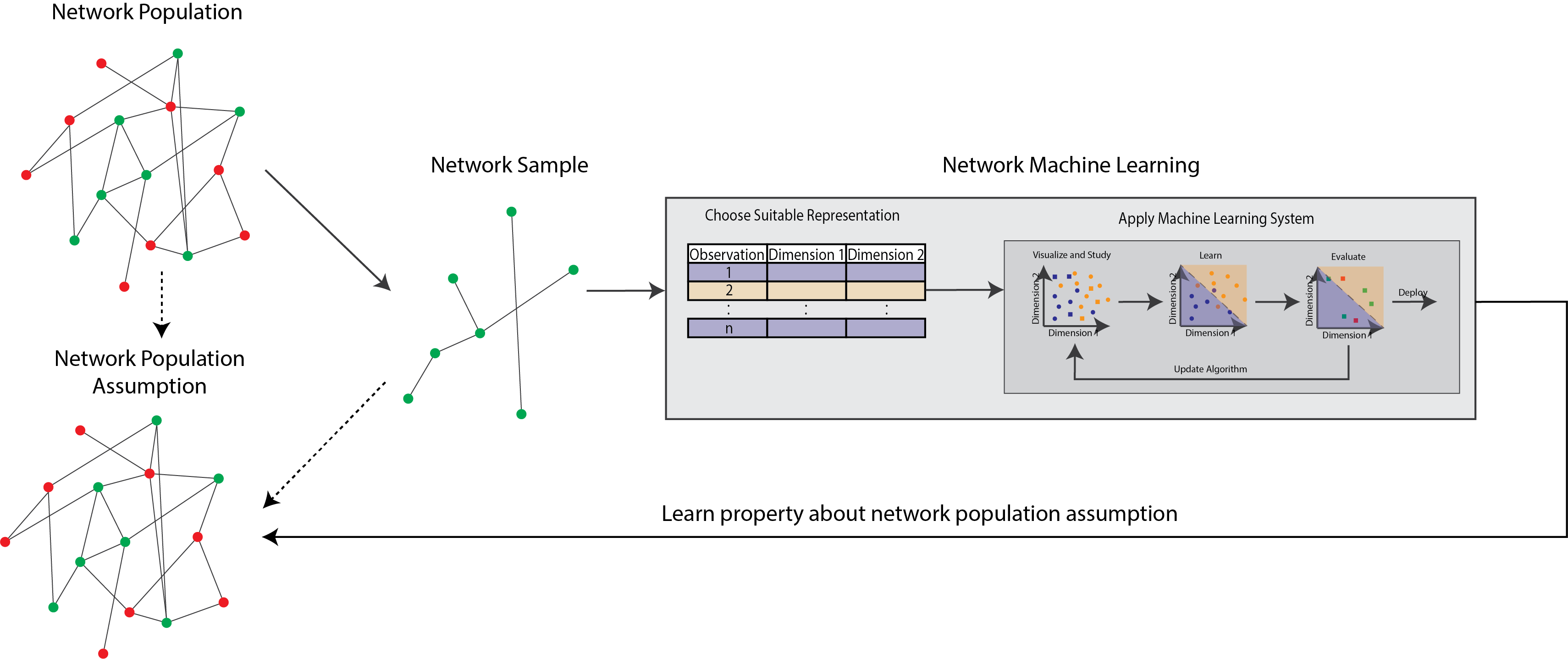
Fig. 1.15 As you can probably tell by now, we have been building up the same figure repeatedly throughout this section to set the tone for how network machine learning works. We have a network population, which in this case, means a set of a potentially infeasibly large network for which we cannot possibly collect the entire network. Note that the network population may have a different interpretation depending on you sepecific network question, and might be populations of many networks, or populations of networks with some level of randomness or uncertainty as to how the network was obtained. You obtain a sample of this network, and then you use your analyses about this sample and your knowledge of how this sample was taken from the population to construct a network population assumption. Ideally, this will faithfully represent the actual network population itself. After analyzing using network machine learning, you learn a property about the network population assumption which you constructed. To do this, we draw from techniques across network science, statistical learning, and data science, as shown in Fig. 2.

We’ll remind you of this later on, but it’s important to note that you can learn lots of valuable things about a sample without using statistics at all, and we will be sure to note when that is the case. However, if you want your conclusions to apply more broadly to the general population rather than the specific sample you collected, a reasonable way to do that quantitatively is using statistical learning.

1.4.3. There are a variety of other challenges too!

In the previous Section 1.3, you learned about some of the different types of network machine learning problems that we can start to address. It’s important to note that, with network machine learning in its infancy, these types of problems are constantly evolving. Just a few years ago, it was totally unknown how to even begin to study many of these problems. As the science has come around, several of these problem types have gradually become more and more prominent. Deciding which group of categories your problem falls into, reshaping your question of interest to fit into problems that can be answered with existing techniques, the types of strategies that are at your disposal to answer your questions, or whether you need to develop new techniques all together to answer your question take lots of energy (and compute resources!). In the next few chapters, you’ll see what example data analyses look like in network machine learning, which will hopefully give you a better idea of how these analyses tend to be performed.