1.3. Types of Network Machine Learning Problems#

There are many different types of network machine learning systems. We tend to broadly group them into the following categories:

  • whether or not they involve one or multiple networks (single or multiple network learning systems),

  • whether or not they require additional information in the form of network attributes (attributed or non-attributed network learning systems),

  • whether they ask questions about an edge, a node, a group of edges/nodes, or about the network itself, and

  • whether or not the approach can be used in isolation from a statistical model (non-model based or model-based network learning systems).

Let’s learn a little bit more about each of these criteria.

1.3.1. Bag of edges, bag of nodes, or whole network#

When you ask questions in machine learning, it’s often the case that your question can be answered without using all of the information about that network that you have at your disposal.

1.3.2. Single vs multiple network learning systems#

1.3.2.1. Single network learning systems#

In many cases of network learning, you only actually have a single sample: the network itself. A single network learning system is a system in which insight is derived from a single network, one collection of nodes and edges. In a single network learning system, you only have one sample: the network itself. In a traditional machine learning framework, having a single sample is disasterous: you canot derive insight with one sample in a traditional machine learning framework, for the simple reason that a question cannot be addressed using only one data point. This is an extreme case of the small sample problem. As an example, if you wanted to determine the degree to which cloud cover predicted whether or not it was raining, and you only had one day worth of data, you would not be able to learn anything without additional information, because your answer would totally be determined by whether or not it was cloudy on that particular day and whether or not it was raining on that particular day.

On the other hand, in network learning, a single sample is far from disasterous. This is because while we only have one network, that one network is defined by a collection of nodes and edges. In order for this to be meaningful, there must be multiple nodes and edges in the first place! This means that while you might only have one network, you can still learn about relationships that exist amongst the nodes, edges, or both. The caveat is that the conclusions you reach from your network might be limited in their application to the specific network you are studying, or a rather limited sample population, but often that’s not much of a problem.

Most of the strategies in this book address single network learning systems.

1.3.2.2. Multiple network learning systems#

In yet other cases of network learning, you might be less restricted. A multiple network learning system is a system in which insight is derived from multiple networks, wherein you have multiple collections of nodes and edges. Unlike a single network learning system in which you can only obtain conclusions on the basis of characteristics of that particular netework itself, in a multiple network learning system, you can obtain insights both within and across the networks.

Let’s consider an example where you have a collection of brain networks from many different people. The nodes of the network represent areas of the brain, and the edges represent whether a pair of areas of the brain can communicate using neurons, which are cells in the brain that receive sensory input from the environment, and transform this sensory input into usable outputs (thoughts, actions, behaviors, etc.) for the rest of the body. Each brain network is from either a musician or a non-musician. You can derive insights to describe the commonalities amongst the brain networks of non-musicians people and the commonalities among the brains of people with musicians, and then compare them to look for differences between the brain networks of non-musicians and musicians.

Some strategies which employ multiple network learning systems are:

1.3.3. Non-attributed vs richy-attributed network learning systems#

In machine learning, you are probably very familiar with the terms unsupervised and supervised learning. In network learning, we tend to use a slightly more specific name for these two ideas.

1.3.3.1. Non-attributed network learning systems#

The concept of a non-attributed network learning system is directly analogous to the concept of fully unsupervised machine learning. Unsupervised learning can be loosely defined as a learning problem in which the data you feed to the algorithm does not include the desired solutions, called labels. We call a network learning system non-attributed if at the time of analysis, the network(s) you feed your algorithm includes only nodes and edges.

For instance, an example that you will see come up several times throughout this book is a school network, in which you have a collection of students who represent the nodes of the network and a collection of edges which represent whether a given pair of students are friends. You hypothesize that there might be two groups of students in the network, called communities, where if a student is in particular group, they tend to be better friends with other students also in that group. You want to see if you can identify these communities programmatically.

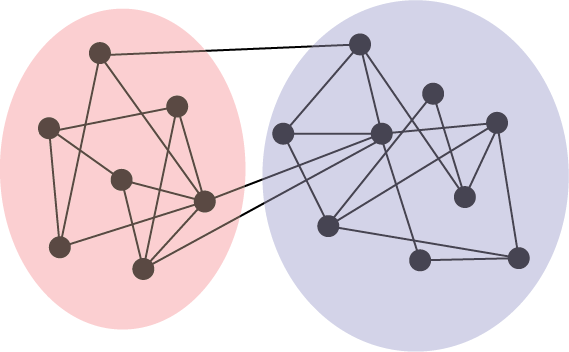
../../_images/nonattr_ex.png

Fig. 1.5 A school network, where the nodes are students and the edges indicate which pairs of students are friends. You hypothesize that there are two communities of students in the network, which might be indicated by the transparent red and blue groups, respectively.#

Some examples of non-attributed network learning systems are:

1.3.3.2. Attributed network learning systems#

Similarly, the concept of an attributed network learning system is analogous to the concept of supervised or semi-supervised machine learning. Supervised learning can be loosely defined as a learning problem in which the data you feed to the algorithm includes labels, and semi-supervised learning can be loosely defined as a learning problem in which the data you feed to the algorithm includes some of the labels. An attributed network learning system if at the time of analysis, the network(s) you feed your algorithm include attributes in addition to nodes and edges. We have four main types of attributed network learning systems. They are:

  • Networks with edge attributes,

  • Networks with node attributes,

  • Networks with network attributes, and

  • Networks with multiple-network attributes.

1.3.3.2.1. Networks with edge attributes#

A network with edge attributes is a network consisting of nodes and edges where, for each edge, you have an additional piece of information to characterize that edge. For instance, if we return to the school example, each edge is either between two individuals from the same school (a within school edge) or from different schools (a between school edge). You can use this information to downstream describe the respective probabilities that each edge type exists.

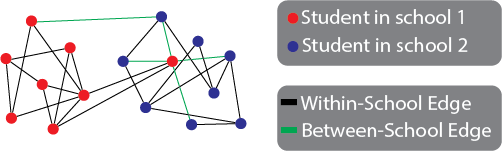
../../_images/edgeattr_ex.png

Fig. 1.6 Two social networks from different social media sites. The nodes are people’s accounts on the social media sites (they are the same for both sites) and the edges indicate which pairs of accounts follow one another for that particular site. For three of the people in the network, you know their accounts.#

An example of a problem which leverages edge attributes is testing for differences between groups of edges in Section 6.2.

1.3.3.2.2. Networks with node attributes#

A network with node attributes is a collection of nodes and edges where, for each node, you have an additional piece of information to describe that node. Let’s consider the school example we talked about above in the section on non-attributed network learning systems. For each student, you also have an additional piece of information: you know which school each student attends, and you want to investigate whether the probability of two students being friends is higher if they are from the same school than if they attend different schools.

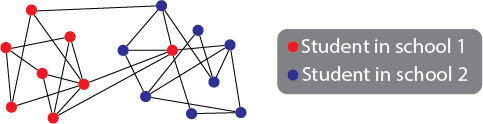
../../_images/nodeattr_ex.png

Fig. 1.7 A school network, where the nodes are students and the edges indicate which pairs of students are friends. For each student, you also know which school the student attends.#

Some examples of problems which deal with node attributes are:

1.3.3.2.3. Networks with network attributes#

A network with network attributes is a collection of networks (each of which has nodes and edges) where, for each network, you have an additional piece of information to characterize that network. For instance, if we return back to the brain networks example we learned about above, each brain network was from either a healthy individual or an individual with a mental illness. This piece of information characterizes each of the entire networks as either from a healthy or mentally ill individual, and applies to the entire collection of nodes and edges for a given network.

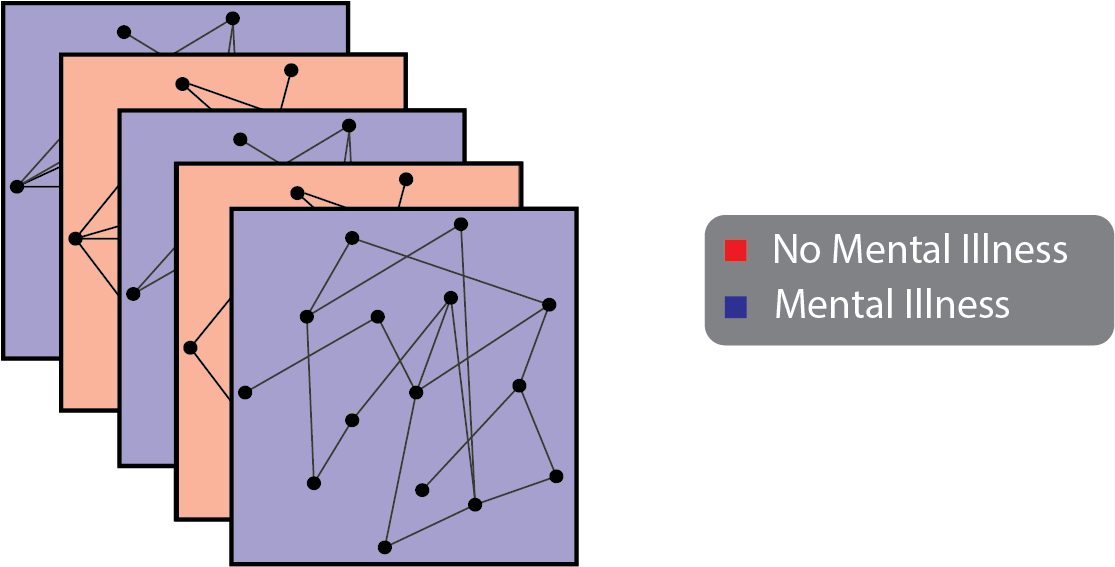
../../_images/netattr_ex.png

Fig. 1.8 A collection of brain networks, where the nodes are areas of the brain and the edges indicate which brain areas can communicate. For each network, you know whether it comes from a healthy person or a patient with mental illness.#

An example of a problem which leverages network attributes are signal subgraphs in Section 8.2.

1.3.3.2.4. Networks with multiple-network attributes#

A network with multiple-network attributes is a collection of networks (each of which has nodes and edges) where you have additional information which describes how the nodes (or the edges) of the networks relate to one another. For instance, let’s consider an example where you have two social networks from different social media sites. The nodes of the network are people’s acounts on the different sites, and the edges indicate which pairs of accounts follow one another for that particular site. The accounts are, for all intents and purposes, anonymous, in that people choose not to share identifying information about themselves on the accounts. However, for three of the people, you know their two accounts that are matched together. You want to see if you can use this cross-network attribute (the matched accounts) to discover suitable matchings for the remaining accounts in the network.

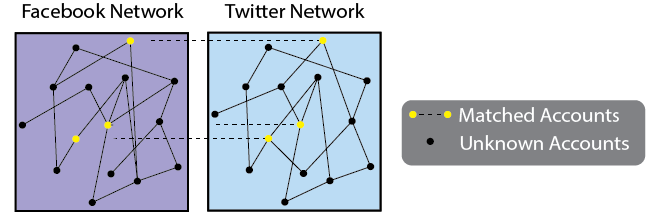
../../_images/crossnetattr_ex.png

Fig. 1.9 Two social networks from different social media sites. The nodes are people’s accounts on the social media sites (they are the same for both sites) and the edges indicate which pairs of accounts follow one another for that particular site. For three of the people in the network, you know their accounts.#

An example of problems which leverage cross-network attributes include:

1.3.4. Whether the questions asks about an edge, a node, group of edges/nodes, or the network itself#

In network machine learning, it’s easy to get lost in the mix of wanting to explore the entire network, when your question might be far more limited. For instance, in a transportation network, you might have a collection of nodes representing stations, and a collection of edges representing the number of riders per train during rush hour. You might have a single network for each week of the entire year. We’ll show an example of each type of question from the perspective of the attributes of these networks. You might want to know whether a particular edge between two stations could require an additional train because it is popular during rush hour, and you might only want to study this particular edge over many networks to get some idea of how many passengers take each train (studying a single edge). You might want to explore the number of passengers which pass through a particular station when deciding whether to approve or reject the expansion of a particular station to include more platforms (studying a single node). You might consider cancelling an entire line all together, and need to think about the ramifications on other stations (groups of nodes) and numbers of passengers per line (groups of edges) of this decision. Alternatively, you might need to determine whether more funds need to be allocated to public transportation as a whole, and need to study how much transportation via the network saves the city over the course of the year (studying properties of the entire network).

1.3.5. Model-based vs non-model-based network learning systems#

As you learned in the previous subsection, statistics tends to form somewhat of a “core” to network learning systems. This is because in any network learning problem, there is always room for randomness, whether it comes in the form of the particularities of the network you sampled, the set of networks you acquired, the nature of the data you collected, or many other factors. We will see a more rigorous definition later on, but for now, you can understand a statistical model to be a conceptual framework of a problem that allows for variation, randomness, or error, to occur in your sample (the data you actually obtain) as compared to the entirety of the actual object or set of objects that you are studying (the population).

1.3.5.1. Non-model-based network learning systems#

For many questions you might want to ask, you could apply techniques from this book in a model-based or non-model-based manner and be just fine. What we mean by this is that a lot of questions might be made intuitive using a model, but there is no reason you need a model in order to answer these questions. A non-model-based network learning system is a system in which a statistical model is not required in order to derive meaning from an analysis.

To explain this point, we will take a brief look at an approach which we will see arise in Section 5 called an adjacency spectral embedding in Section 5.3, or ASE. Let’s say that you have a network, and you want to see if there are groups of nodes that can be clustered together using K-means. K-means is a machine learning technique which needs tabular data, which as you saw in the preceding section, are those in which you have observations and features organized in rows and columns, and can apply traditional machine learning techniques readily. An ASE is one of many techniques that you can use in order to take a network, and obtain a tabular representation of the network where the observations are nodes of the network. While using a statistical model would allow you to derive insight into what exactly the tabular representation of the data intuitively is capturing of the nodes, you can apply ASE in isolation from the statistical model, and just apply K-means to obtain your result. In this sense, ASE is a procedure which produces a desired result.

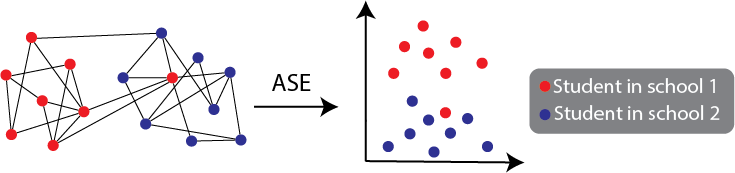
../../_images/ase_ex.png

Fig. 1.10 Two social networks from different social media sites. The nodes are people’s accounts on the social media sites (they are the same for both sites) and the edges indicate which pairs of accounts follow one another for that particular site. For three of the people in the network, you know their accounts.#

To make this type of machine learning system a little more concrete, we’ll break down a more traditional non-model-based machine learning system and show a similar relationship. If you are reading this book, we anticipate you have probably come across Principal Components Analysis, or PCA. If you have not, principal components analysis is simply a procedure which takes data which is big (it has a lot of features or dimensions which is extremely problematic for many machine learning approaches) and makes it small (it has a manageable number of features or dimensions) so that you can use other strategies downstream which might be more reasonable. By more reasonable, what we mean is that each observation starts with many features, and after applying PCA, each observation has far fewer features.

There is no reason that this procedure cannot be executed knowing nothing else about the data: it is simply an algorithm which produces a desired result (making the data manageable for other machine learning techniques). However, if you were to do this and use the intuition of a statistical model (specifically, that the observations are normally distributed), you can understand the principal components to be representations of the data that preserve the most variation. The degree of variation preserved by the principal components, if you recall, are indicated by the principal component scores. This is often desirable intuition for machine learning because if you wanted to apply say K-Means to cluster your observations, you will need the observations from each class to “look” different, and “looking different” requires variability.

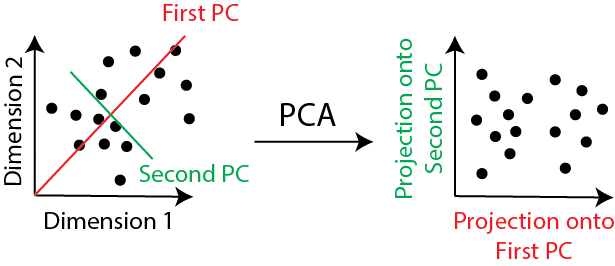
../../_images/pca_ex.png

Fig. 1.11 Two social networks from different social media sites. The nodes are people’s accounts on the social media sites (they are the same for both sites) and the edges indicate which pairs of accounts follow one another for that particular site. For three of the people in the network, you know their accounts.#

1.3.5.2. Model-based network learning systems#

On the other hand, sometimes questions can only be understood, conceptualized, or addressed using a statistical model. A model-based network learning system is a system in which a statstical model is required in order to derive your intended meaning from an analysis.

We don’t quite expect you to be ready to understand the nuances of this type of network learning system just yet, so we will give an example from a more standard model-based machine learning system. Imagine that you have two coins, and you flip each of them twenty times. You want to understand whether the probability that the two coins land on heads are the same or different. What this means in statistics is that you want to perform a hypothesis test: you want to use the data that you obtained (the outcomes of the twenty coin flips for each of the two coins) to determine whether the coins have the same probability of landing on heads (the first hypothesis) or a different probability of landing on heads (the second hypothesis). The hypothesis test is the procedure to determine which of the two hypotheses is better supported by the data that you have. This question cannot really be made sense without using a statistical model, because the term probability has a statistical interpretation. If you wanted to answer this question, you would need to describe the experiment a little bit further. We provide some of the details you would need to know below:

  • Can each of the coins only land on heads or tails, or is there perhaps some other outcome that’s possible? For instance, is one of the coins one centimeter thick and the other a picometer thick, and therefore, the centimeter thick coin has a nonzero probability of landing on its side?

  • For each coin, is the probability that the coin lands on heads exactly the same across each of your twenty coin flips for that particular coin? For example, if you flip the coin differently for the first ten flips than you do on the last ten flips, could this artificially make the coin land on heads more or less frequently?

  • Do the outcomes of the coin flips depend on other coin flips? For instance, if you see two straight tails in one of the coins and say a prayer that you get a heads on the next flip, does this impact the probability that the next flip is a heads?

In order to make a conclusion based on your hypothesis test, you need to be really specific about your assumptions for these details of the sample of data that you have, since if any of your assumptions turn out to be untrue, the answer to your question might have an interpretation that is slightly different. Therefore, you need to understand the assumptions that you made, so that you can make a decision based on the outcome of the hypothesis test that you performed.

1.3.6. Combine and conquer#

It is important to note that none of these categories are mutually exclusive, and a network machine learning system will pull elements from several of the different categories simultaneously. For instance, you might have a machine learning system that is a single network, node-attributed, non-model-based machine learning system like a community detection algorithm.