Why Use Statistical Models?
4. Why Use Statistical Models?#
At the foundation of statistical inference is the statistical model. This concept can seem somewhat esoteric, and often times, the word “statistical model”, we find, is a bit overused. However, it is extremely important to clarify exactly what a statistical model is, and what it isn’t, so we hope to clear up some of those misconceptions here before we jump in. A statistical model is, at its core, purely theoretical in nature. Statistical models fit into the network learning pipeline like this:
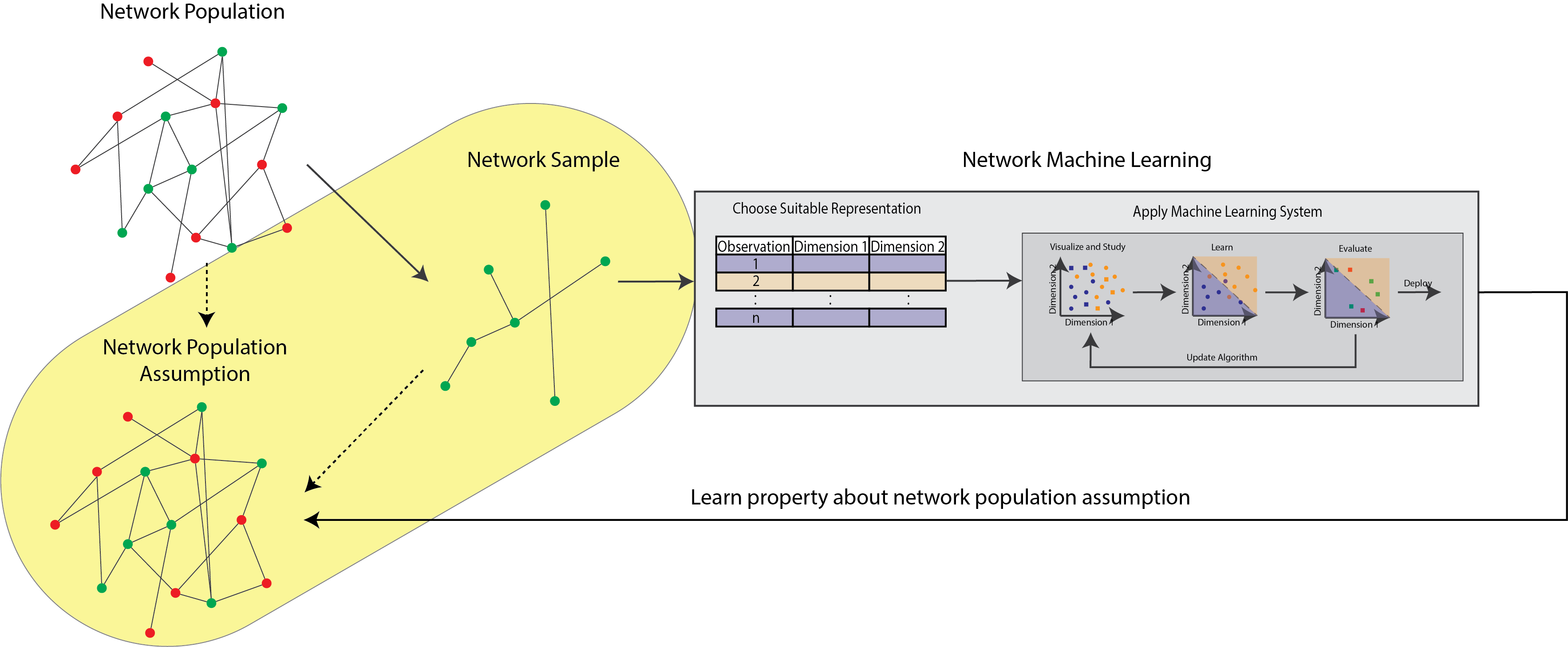
Fig. 4.1 In this chapter, you will learn how to construct sets of assumptions about the network which underlies your network sample.#
The reality is, the network you observe, which you learned how to describe in the previous chapter, is not typically the thing you want to learn about. Rather, you want to learn about the system which underlies the network you observed. To learn about the dynamics of this system is a three-step process: first, you need to assume some things about the system (this chapter); second, you need to learn representations of the network you see that will be useful to you (the next chapter), and finally, you need to learn how that representation can inform the assumptions you made about the system. This process can be boiled down quite a bit to how flipping a coin works. When you flip a coin, usually you don’t know ahead of time whether that coin is going to land on heads or tails. Instead, you think that coin is going to land on heads or tails with some probability (usually, an even chance of landing on heads or tails, or a probability of \(0.5\)). If you flip the coin once and get heads, you don’t think that coin is only going to ever land on heads: rather, you think that coin landed on heads because of some amount of random chance.
And herein, you just assumed a statistical model. You assumed that the outcome of your coin (the random object, here, that you are modelling) was heads or tails with some probability, and when you saw that outcome (the sample of the coin flip) you prescribed that outcome to one of the possible outcomes occuring. As you’ll see briefly, network modelling is nearly the same, and for simple networks especially, is exactly the same as flipping coins. Throughout this chapter, you’ll learn to think about each edge of the network as a particular coin. Remember that the edges for a simple (and consequently, unweighted) network either exist or they don’t exist: this is exactly like a coin landing on heads or tails. The key difference is that the edges existing or not existing might happen at probabilities different from \(0.5\); there might be a chance of \(0.7\) that one edge exists, or \(0.4\) that another edge exists.
When you construct models for networks, what you are going to do is prescribe sets of assumptions for how the coin for each edge behaves: are all of the edges in the network flipping coins with equal probability (do all the edges exist or not exist with the same chance)? Are there some groups of nodes whose edges all have the same probabilities? Are there other ways you can describe the probabilities that other edges exist or do not exist? We’ll learn about the following models, which tend to be some of the more common simple network models for network learning:
Network modelling can get pretty dicey in the mathematics rather quickly. For this reason, for the main text of the book, we’ve tried to keep the level of mathematical depth required as low as possible, so that you can focus more on the intuition and less on the mathematical rigor. For the more technical readers, Section 11 provides more in-depth coverage of statistical network models. In this appendix section, we cover rigorous, statistical, descriptions of the statistical models and other concepts such as the likelihood function.

