Properties of Networks as a Statistical Object
3. Properties of Networks as a Statistical Object#
In this section, you’ll learn the basics of network-valued data. As you saw in the introduction, for many reasons, network valued data is fundamentally different from other forms of data, such as tabular data, that are often used in machine learning. Back in Section 1.4, we introduced you to a figure which is going to come up repeatedly throughout this book, so that we can contextualize where we are in the process of learning how to learn from networks. The figure looked something like this:
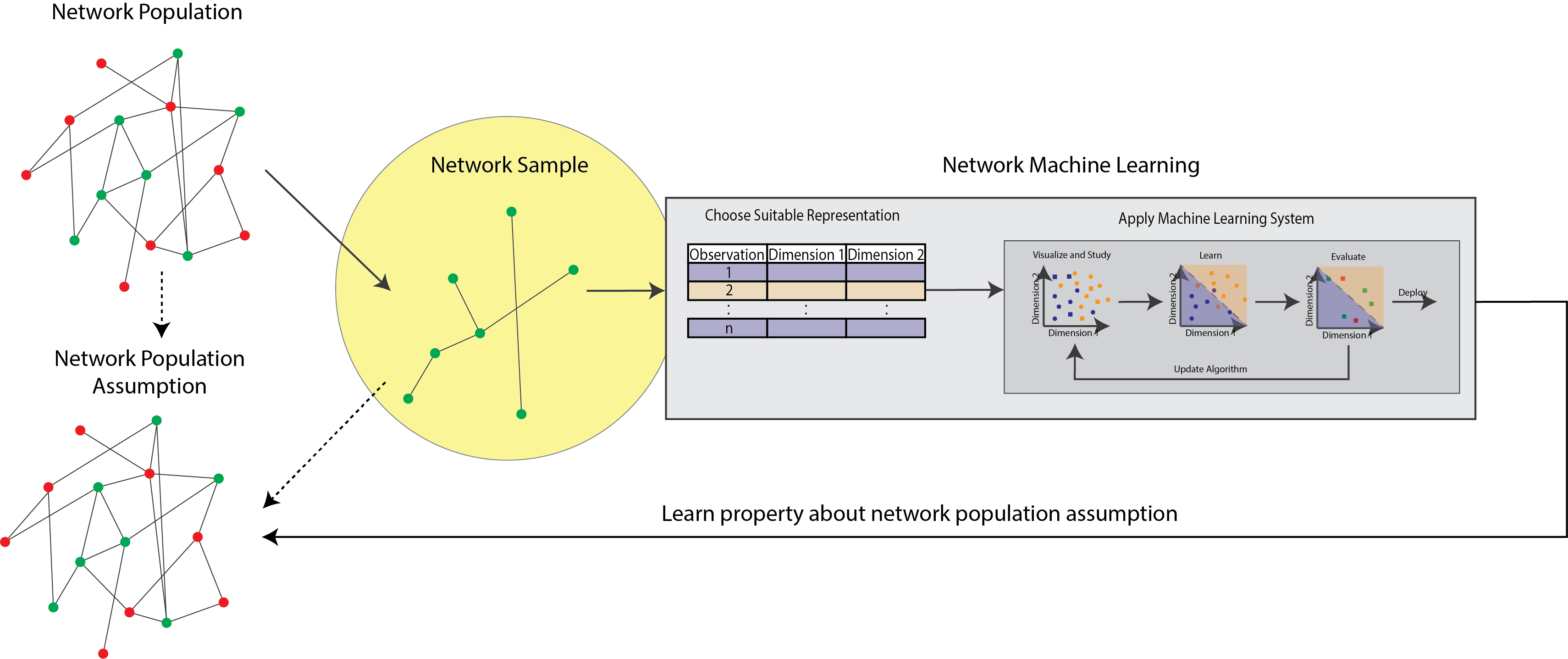
Fig. 3.1 The statistical learning pipeline. In this chapter, you will learn about how to describe the network you observe in your analysis.#
When you try to learn from a network that you see through your research, your work, or anywhere else, the first thing to do is to know exactly how to describe that network. This network that you see is known as a sample or an observation of a network. The reason we call it an observation or a sample of a network is that the network you see is never going to perfectly describe the process you are trying to study. No matter what, there will always be some level of noise. However, before we start to learn how to characterize that noise and perhaps better describe the observed network, you need to learn how to describe the network you observe first. Throughout the subsections, you’ll learn about the fundamental representation we use for networks in this book, which is called the adjacency matrix. The reason we turn to adjacency matrices extremely often in network machine learning is that they tend to have nice mathematical properties; particularly, that the matrix is the fundamental unit for linear algebra, a subset of mathematics that you might have become introduced to in your mathematical courses. When you apply algorithms to networks, more often than not, you can use linear algebra techniques to describe the operation mathematically and in a precise way that allows you to apply the algorithm en masse to the entire network. We have the following subsections we’ll cover:

