Calculating pAUC

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.metrics import roc_auc_score, roc_curve

from sktree.datasets import make_trunk_classification
from sktree.ensemble import HonestForestClassifier
from sktree.stats import build_oob_forest

sns.set(color_codes=True, style="white", context="talk", font_scale=1.5)
PALETTE = sns.color_palette("Set1")
sns.set_palette(PALETTE[1:5] + PALETTE[6:], n_colors=9)
sns.set_style("white", {"axes.edgecolor": "#dddddd"})

pAUC@r

Partial area under the ROC curve (pAUC) integrates the true positive rates (TPR) when the false positive rates (FPR) are below a specific percentage threshold. Then the value is normalized by that percentage.

\[pAUC@r = \frac{100}{100 - r} \int_{T_r}^\infty \int_{\mathcal{X}} \mathbb{I}\{\eta(X_1) > \eta(X_0) \} dF_1 dF_0\]

With a binary class simulation as an example, this tutorial will show how to use treeple to calculate the statistic with 90% specificity threshold.

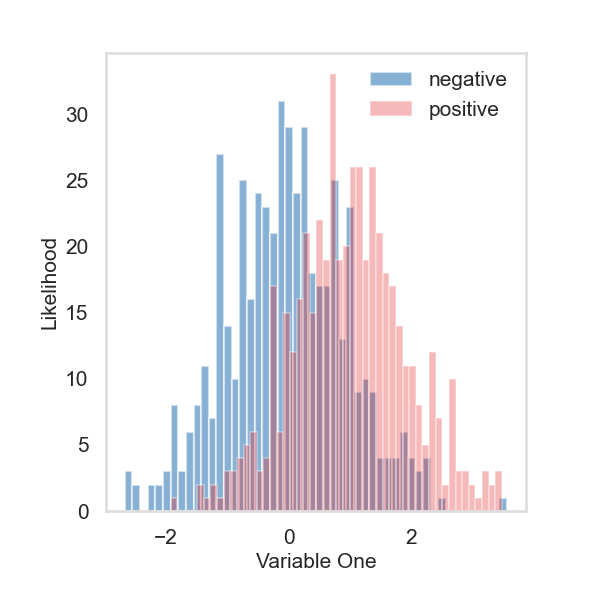
Create a simulation with two gaussians

# create a binary class simulation with two gaussians
# 500 samples for each class, class zero is standard
# gaussian, and class one has a mean at one
X, y = make_trunk_classification(
    n_samples=1000,
    n_dim=1,
    mu_0=0,
    mu_1=1,
    n_informative=1,
    seed=1,
)


fig, ax = plt.subplots(figsize=(6, 6))
fig.tight_layout()
ax.tick_params(labelsize=15)

# histogram plot the samples
ax.hist(X[:500], bins=50, alpha=0.6, color=PALETTE[1], label="negative")
ax.hist(X[500:], bins=50, alpha=0.3, color=PALETTE[0], label="positive")
ax.set_xlabel("Variable One", fontsize=15)
ax.set_ylabel("Likelihood", fontsize=15)
plt.legend(frameon=False, fontsize=15)
plt.show()

Fit the model

# initialize the forest with 100 trees
est = HonestForestClassifier(
    n_estimators=100,
    max_samples=1.6,
    max_features=0.3,
    bootstrap=True,
    stratify=True,
    random_state=1,
)

# fit the model and obtain the tree posteriors
_, observe_proba = build_oob_forest(est, X, y)

# generate forest posteriors for the two classes
observe_proba = np.nanmean(observe_proba, axis=0)


fig, ax = plt.subplots(figsize=(6, 6))
fig.tight_layout()
ax.tick_params(labelsize=15)

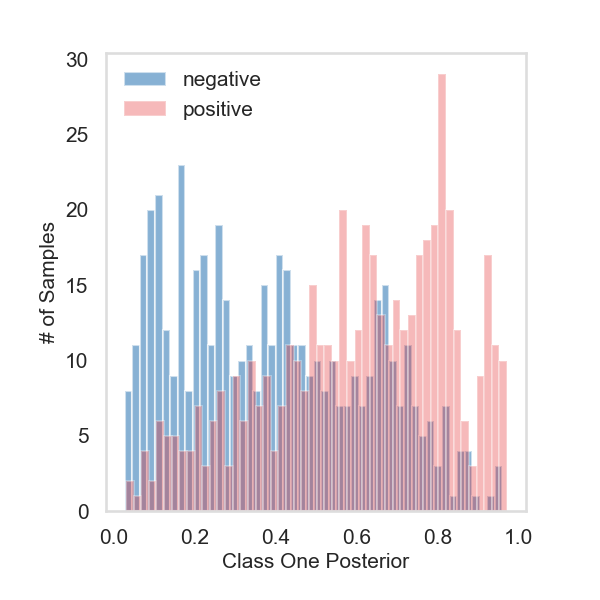
# histogram plot the posterior probabilities for class one
ax.hist(observe_proba[:500][:, 1], bins=50, alpha=0.6, color=PALETTE[1], label="negative")
ax.hist(observe_proba[500:][:, 1], bins=50, alpha=0.3, color=PALETTE[0], label="positive")
ax.set_ylabel("# of Samples", fontsize=15)
ax.set_xlabel("Class One Posterior", fontsize=15)
plt.legend(frameon=False, fontsize=15)
plt.show()

Calculate the statistic

def Calculate_pAUC(y_true, y_pred_proba, max_fpr=0.1) -> float:
    # check the shape of true labels
    if y_true.squeeze().ndim != 1:
        raise ValueError(f"y_true must be 1d, not {y_true.shape}")

    # find the positive class and calculate fpr and tpr
    if 0 in y_true or -1 in y_true:
        fpr, tpr, thresholds = roc_curve(
            y_true, y_pred_proba[:, 1], pos_label=1, drop_intermediate=False
        )
    else:
        fpr, tpr, thresholds = roc_curve(
            y_true, y_pred_proba[:, 1], pos_label=2, drop_intermediate=False
        )

    fig, ax = plt.subplots(figsize=(6, 6))
    fig.tight_layout()
    ax.tick_params(labelsize=15)
    ax.set_xlim([-0.005, 1.005])
    ax.set_ylim([-0.005, 1.005])
    ax.set_xlabel("False Positive Rate", fontsize=15)
    ax.set_ylabel("True Positive Rate", fontsize=15)

    ax.plot(fpr, tpr, label="ROC curve", color=PALETTE[1])
    # Calculate pAUC at the specific threshold
    pAUC = roc_auc_score(y_true, y_pred_proba[:, 1], max_fpr=max_fpr)

    pos = np.where(fpr == max_fpr)[0][-1]
    ax.fill_between(
        fpr[:pos],
        tpr[:pos],
        color=PALETTE[0],
        alpha=0.6,
        label="pAUC@90 = " + str(round(pAUC, 2)),
        linestyle="--",
    )
    ax.legend(frameon=False, fontsize=15)
    return pAUC


pAUC = Calculate_pAUC(y, observe_proba)
print("pAUC@90 =", round(pAUC, 2))

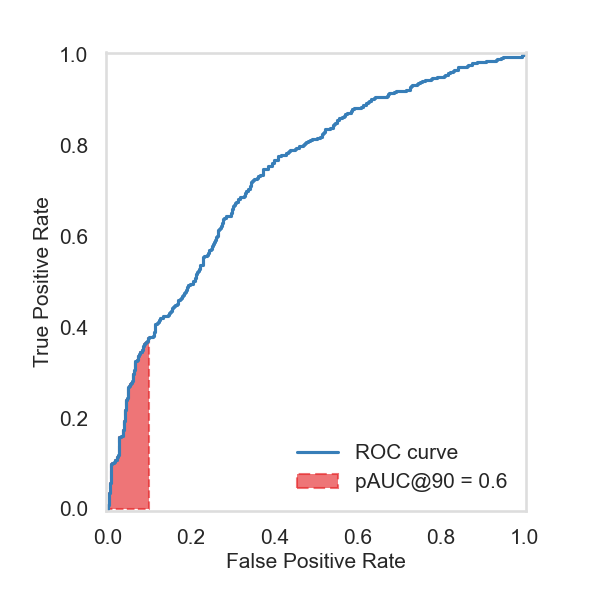
pAUC@90 = 0.6