Recreating Youngser's R code figures
Simulated data experiments showing the effectiveness of graph matching with spectral similarity
# collapse
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.pyplot as plt
import random
import sys
from joblib import Parallel, delayed
from graspy.simulations import sbm_corr
Experiment Summary
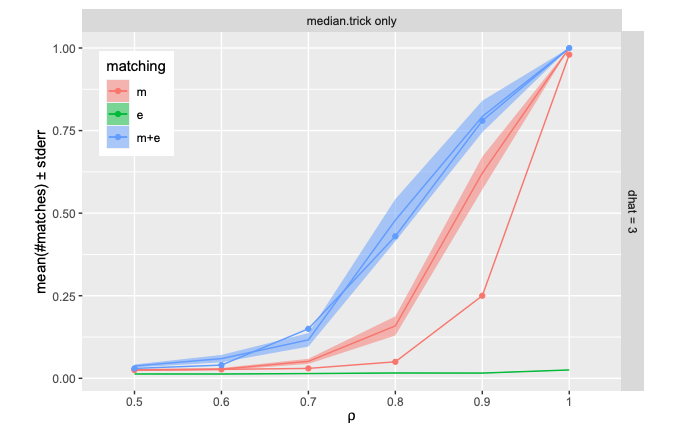
All values were set to best replicate Youngser's Figure
Let $(G_1, G_2) \sim \rho-SBM(\vec{n},B)$. (NB: binary, symmetric, hollow.)
$K = 3$.
the marginal SBM is conditional on block sizes $\vec{n}=[n_1,n_2,n_3]$.
$B = [(.20,.01,.01);(.01,.10,.01);(.01,.01,.20)]$. (NB: rank($B$)=3 with evalues $\approx [0.212,0.190,0.098]$.)
with $n = 150$ and $\vec{n}=[n_1,n_2,n_3] = [50,50,50]$
for each $\rho \in \{0.5,0.6,\cdots,0.9,1.0\}$ generate $r$ replicates $(G_1, G_2)$.
For all $r$ replicates, run $GM$ and $GM_{SS}$ each $t$ times, with each $t$ corresponding to a different random permutation on $G_2$.
Specifically,$G_2' = Q G_2 Q^T,$ where $Q$ is sampled uniformly from the set of $n x n$ permutations matrices.
For each $t$ permutation, run $GM$ & $GM_{SS}$ from the barycenter ($\gamma = 0$).
For each $r$, the $t$ permutation with the highest associated objective function value will have it's match ratio recorded
For any $\rho$ value, have $\delta$ denote the average match ratio over the $r$ realizations
Plot $x=\rho$ vs $y$= $\delta$ $\pm$ s.e.
This notebook contains figures for $r=50$, $t=10$
NOTE: The max number of FW iterations here is set at 20 to best replicate Youngser R results.
# collapse
ratios = np.genfromtxt('ratios.csv', delimiter = ',')
ratios_ss = np.genfromtxt('ratios_ss.csv', delimiter=',')
scores = np.genfromtxt('scores.csv', delimiter = ',')
scores_ss = np.genfromtxt('scores_ss.csv', delimiter=',')
rhos = np.arange(5,10.5,0.5) *0.1
odds = [i for i in range(len(rhos)) if i%2==0]
n_p = len(rhos)
# collapse
from scipy.stats import sem
import seaborn as sns
error = np.asarray([sem(ratios[i,:]) for i in range(n_p)])
average = np.asarray([np.mean(ratios[i,:] ) for i in range(n_p)])
error_ss = np.asarray([sem(ratios_ss[i,:]) for i in range(n_p)])
average_ss = np.asarray([np.mean(ratios_ss[i,:] ) for i in range(n_p)])
# collapse
sns.set_context('paper')
sns.set(rc={'figure.figsize':(12,8)})
plt.errorbar(rhos[odds],average_ss[odds], error_ss[odds],marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GM+SS', color='blue')
plt.errorbar(rhos[odds],average[odds], error[odds],marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GM', color='red')
plt.xlabel("rho")
plt.ylabel("avergae match ratio")
plt.text(0.5,0.5, 'r=50, t=10')
plt.legend()
# collapse
gm_ss_y = [0.01, 0.03, 0.12, 0.42, 0.77, 1.0]
gm_y = [0, 0, 0.03, 0.15, 0.62, 1.0]
sns.set_context('paper')
sns.set(rc={'figure.figsize':(12,8)})
plt.errorbar(rhos[odds],average_ss[odds], error_ss[odds],marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GM+SS', color='blue')
plt.plot(rhos[odds],gm_ss_y, color='blue', marker='^')
plt.errorbar(rhos[odds],average[odds], error[odds],marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GM', color='red')
plt.plot(rhos[odds],gm_y, color='red', marker='^')
plt.xlabel("rho")
plt.ylabel("avergae match ratio")
plt.text(0.5,0.5, 'triangles = youngser, circle = ali')
plt.legend()
# collapse
ratios_opt = np.genfromtxt('ratios_opt.csv', delimiter = ',')
ratios_opt_ss = np.genfromtxt('ratios_opt_ss.csv', delimiter=',')
scores_opt = np.genfromtxt('scores_opt.csv', delimiter = ',')
scores_opt_ss = np.genfromtxt('scores_opt_ss.csv', delimiter=',')
rhos = np.arange(5,10.5,0.5) *0.1
n_p = len(rhos)
Call 'best case' the instance where $Q$ sampled uniformly from the set of $n x n$ permutations matrices is equal to the identity matrix.
As we see from the figures below, for vanilla GM, the best case seems to consistently perform better, but with GM+SS they appear to be consistently about the same
# collapse
diff = scores_opt_ss[9,:] - scores_ss[9,:]
plt.hist(diff, bins=10)
plt.vlines(0,0,50,linestyles='dashed', color = 'red', label='x=0')
plt.ylabel('Density')
plt.xlabel('Objective Value Difference ("Best Case" - argmax_t[objective_t])')
plt.title('Paired Difference Histogram (Rho = 0.9)')
# collapse
diff = ratios_opt_ss[9,:] - ratios_ss[9,:]
plt.hist(diff, bins=10)
plt.vlines(0,0,50,linestyles='dashed', color = 'red', label='x=0')
plt.ylabel('Density')
plt.xlabel('Match Ratio Difference ("Best Case" - argmax_t[objective_t])')
plt.title('Paired Difference Histogram (Rho = 0.9)')
# collapse
diff = scores_opt[9,:] - scores[9,:]
plt.hist(diff, bins=10)
plt.vlines(0,0,50,linestyles='dashed', color = 'red', label='x=0')
plt.ylabel('Density')
plt.xlabel('Objective Value Difference ("Best Case" - argmax_t[objective_t])')
plt.title('Paired Difference Histogram (Rho = 0.9)')
# collapse
diff = ratios_opt[9,:] - ratios[9,:]
plt.hist(diff, bins=10)
plt.vlines(0,0,50,linestyles='dashed', color = 'red', label='x=0')
plt.ylabel('Density')
plt.xlabel('Match Ratio Difference ("Best Case" - argmax_t[objective_t])')
plt.title('Paired Difference Histogram (Rho = 0.9)')
# collapse
import numpy as np
import matplotlib.pyplot as plt
import random
import sys
from joblib import Parallel, delayed
from .qap_sim import quadratic_assignment_sim
import seaborn as sns
from graspy.match import GraphMatch as GMP
from graspy.simulations import sbm_corr
def run_sim(r, t):
def match_ratio(inds, n):
return np.count_nonzero(inds == np.arange(n)) / n
n = 150
m = r
#rhos = 0.1 * np.arange(11)[5:]
rhos = np.arange(5,10.5,0.5) *0.1
n_p = len(rhos)
ratios = np.zeros((n_p,m))
scores = np.zeros((n_p,m))
ratios_ss = np.zeros((n_p,m))
scores_ss = np.zeros((n_p,m))
ratios_opt = np.zeros((n_p,m))
scores_opt = np.zeros((n_p,m))
ratios_opt_ss = np.zeros((n_p,m))
scores_opt_ss = np.zeros((n_p,m))
n_per_block = int(n/3)
n_blocks = 3
block_members = np.array(n_blocks * [n_per_block])
block_probs = np.array([[0.2, 0.01, 0.01], [0.01, 0.1, 0.01], [0.01, 0.01, 0.2]])
directed = False
loops = False
for k, rho in enumerate(rhos):
np.random.seed(8888)
seeds = [np.random.randint(1e8, size=t) for i in range(m)]
def run_sim(seed):
A1, A2 = sbm_corr(
block_members, block_probs, rho, directed=directed, loops=loops
)
score = 0
res_opt = None
score_ss = 0
res_opt_ss = None
for j in range(t):
res = quadratic_assignment_sim(A1,A2, sim=False, maximize=True, options={'seed':seed[j]})
if res['score']>score:
res_opt = res
score = res['score']
res = quadratic_assignment_sim(A1,A2, sim=True, maximize=True, options={'seed':seed[j]})
if res['score']>score_ss:
res_opt_ss = res
score_ss = res['score']
ratio = match_ratio(res_opt['col_ind'], n)
score = res_opt['score']
ratio_ss = match_ratio(res_opt_ss['col_ind'], n)
score_ss = res_opt_ss['score']
res = quadratic_assignment_sim(A1,A2, sim=False, maximize=True, options={'shuffle_input':False})
ratio_opt = match_ratio(res['col_ind'], n)
score_opt = res['score']
res = quadratic_assignment_sim(A1,A2, sim=True, maximize=True, options={'shuffle_input':False})
ratio_opt_ss = match_ratio(res['col_ind'], n)
score_opt_ss = res['score']
return ratio, score, ratio_ss, score_ss, ratio_opt, score_opt, ratio_opt_ss, score_opt_ss
result = Parallel(n_jobs=-1, verbose=10)(delayed(run_sim)(seed) for seed in seeds)
ratios[k,:] = [item[0] for item in result]
scores[k,:] = [item[1] for item in result]
ratios_ss[k,:] = [item[2] for item in result]
scores_ss[k,:] = [item[3] for item in result]
ratios_opt[k,:] = [item[4] for item in result]
scores_opt[k,:] = [item[5] for item in result]
ratios_opt_ss[k,:] = [item[6] for item in result]
scores_opt_ss[k,:] = [item[7] for item in result]
np.savetxt('ratios.csv',ratios, delimiter=',')
np.savetxt('scores.csv',scores, delimiter=',')
np.savetxt('ratios_ss.csv',ratios_ss, delimiter=',')
np.savetxt('scores_ss.csv',scores_ss, delimiter=',')
np.savetxt('ratios_opt.csv',ratios_opt, delimiter=',')
np.savetxt('scores_opt.csv',scores_opt, delimiter=',')
np.savetxt('ratios_opt_ss.csv',ratios_opt_ss, delimiter=',')
np.savetxt('scores_opt_ss.csv',scores_opt_ss, delimiter=',')
from scipy.stats import sem
error = [2*sem(ratios[i,:]) for i in range(n_p)]
average = [np.mean(ratios[i,:] ) for i in range(n_p)]
error_ss = [2*sem(ratios_ss[i,:]) for i in range(n_p)]
average_ss = [np.mean(ratios_ss[i,:] ) for i in range(n_p)]
sns.set_context('paper')
#sns.set(rc={'figure.figsize':(15,10)})
txt =f'r={r}, t={t}'
plt.errorbar(rhos,average_ss, error_ss,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GM+SS')
plt.errorbar(rhos,average, error,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GM', color='red')
plt.xlabel("rho")
plt.ylabel("avergae match ratio")
plt.text(0.5,0.5,txt)
plt.legend()
plt.savefig('figure_matchratio.png', dpi=150, facecolor="w", bbox_inches="tight", pad_inches=0.3)