rho-Simulated SBM, n=150,1500¶
#hide
%load_ext autoreload
%autoreload 1
from pkg.gmp import quadratic_assignment
from pkg.gmp import quadratic_assignment_ot
from pkg.plot import set_theme
import numpy as np
import sys
sys.path
sys.path.insert(0,'../../graspologic')
Experiment Summary, n = 150¶
Let \((G_1, G_2) \sim \rho-SBM(\vec{n},B)\). (NB: binary, symmetric, hollow.)
\(K = 3\).
the marginal SBM is conditional on block sizes \(\vec{n}=[n_1,n_2,n_3]\).
\(B = [(.20,.01,.01);(.01,.10,.01);(.01,.01,.20)]\). (NB: rank(\(B\))=3 with evalues \(\approx [0.212,0.190,0.098]\).)
with \(n = 150\) and \(\vec{n}=[n_1,n_2,n_3] = [50,50,50]\)
for each \(\rho \in \{0.5,0.6,\ldots,0.9,1.0\}\) generate \(r\) replicates \((G_1, G_2)\).
For all \(r\) replicates, run \(GM\) and \(GM_{LS}\) (where \(GM_{LS}\) uses the “Lightspeed sinkhorn distances” for computing the step direction) each \(t\) times, with each \(t\) corresponding to a different random permutation on \(G_2\) .
Specifically,\(G_2' = Q G_2 Q^T,\) where \(Q\) is sampled uniformly from the set of \(n x n\) permutations matrices.
For each \(t\) permutation, run \(GM\) & \(GM_{LS}\) from the barycenter (\(\gamma = 0\)).
For each \(r\), the \(t\) permutation with the highest associated objective function value will have it’s match ratio recorded
For any \(\rho\) value, have \(\delta\) denote the average match ratio over the \(r\) realizations
Plot \(x=\rho\) vs \(y\)= \(\delta\) \(\pm\) 2s.e.
Below contains figures for \(r=50\), \(t=10\)
#hide
import numpy as np
import matplotlib.pyplot as plt
import random
import sys
from joblib import Parallel, delayed
import seaborn as sns
# from graspy.match import GraphMatch as GMP
from graspologic.simulations import sbm_corr
# from scipy.optimize import linear_sum_assignment
from sklearn.metrics import pairwise_distances
r = 100
t=10
# gmp = GraphMatch('maximize':True, 'tol':0.000001,'maxiter':30, 'shuffle_input':True)
def match_ratio(inds, n):
return np.count_nonzero(inds == np.arange(n)) / n
n = 150
m = r
rhos = 0.1 * np.arange(11)[5:]
# rhos = np.arange(8,10.5,0.5) *0.1
n_p = len(rhos)
ratios = np.zeros((n_p,m))
scores = np.zeros((n_p,m))
ratios_ss = np.zeros((n_p,m))
scores_ss = np.zeros((n_p,m))
n_per_block = int(n/3)
n_blocks = 3
block_members = np.array(n_blocks * [n_per_block])
block_probs = np.array([[0.2, 0.01, 0.01], [0.01, 0.1, 0.01], [0.01, 0.01, 0.2]])
directed = False
loops = False
for k, rho in enumerate(rhos):
np.random.seed(8888)
seeds = [np.random.randint(1e8, size=t) for i in range(m)]
def run_sim(seed):
A1, A2 = sbm_corr(
block_members, block_probs, rho, directed=directed, loops=loops
)
score = 0
res_opt = None
score_ss = 0
res_opt_ss = None
for j in range(t):
res = quadratic_assignment(A1,A2, options={'maximize':True,'tol':1e-6,'maxiter':50, 'shuffle_input':True})
if res.fun>score:
perm = res.col_ind
score = res.fun
res_ss = quadratic_assignment_ot(A1,A2, options={'maximize':True,'tol':1e-6,'maxiter':50, 'shuffle_input':True, 'reg': 100, 'thr':1e-2})
if res_ss.fun>score_ss:
perm_ss = res_ss.col_ind
score_ss = res_ss.fun
ratio = match_ratio(perm, n)
ratio_ss = match_ratio(perm_ss, n)
return ratio, score, ratio_ss, score_ss
result = Parallel(n_jobs=-1)(delayed(run_sim)(seed) for seed in seeds)
ratios[k,:] = [item[0] for item in result]
scores[k,:] = [item[1] for item in result]
ratios_ss[k,:] = [item[2] for item in result]
scores_ss[k,:] = [item[3] for item in result]
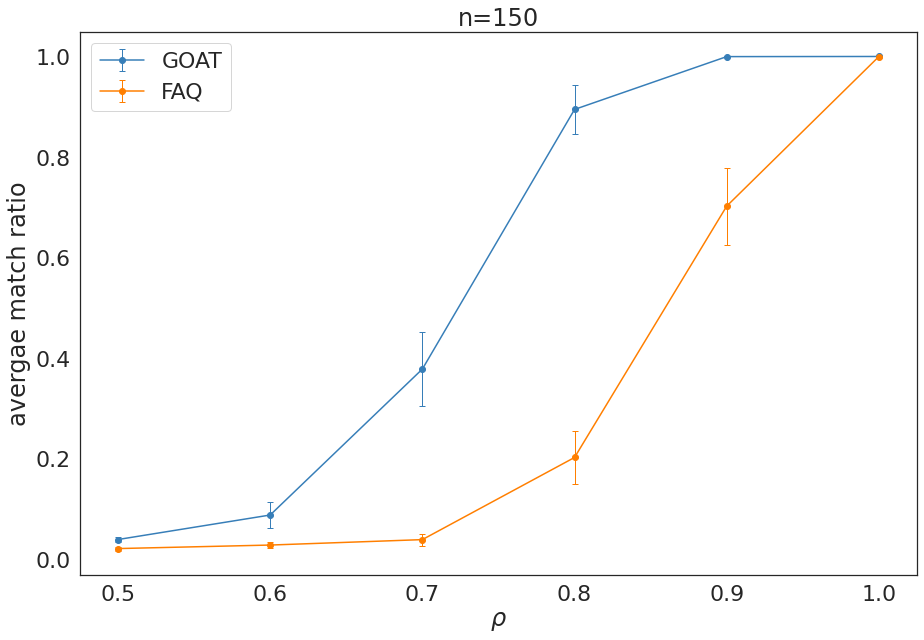
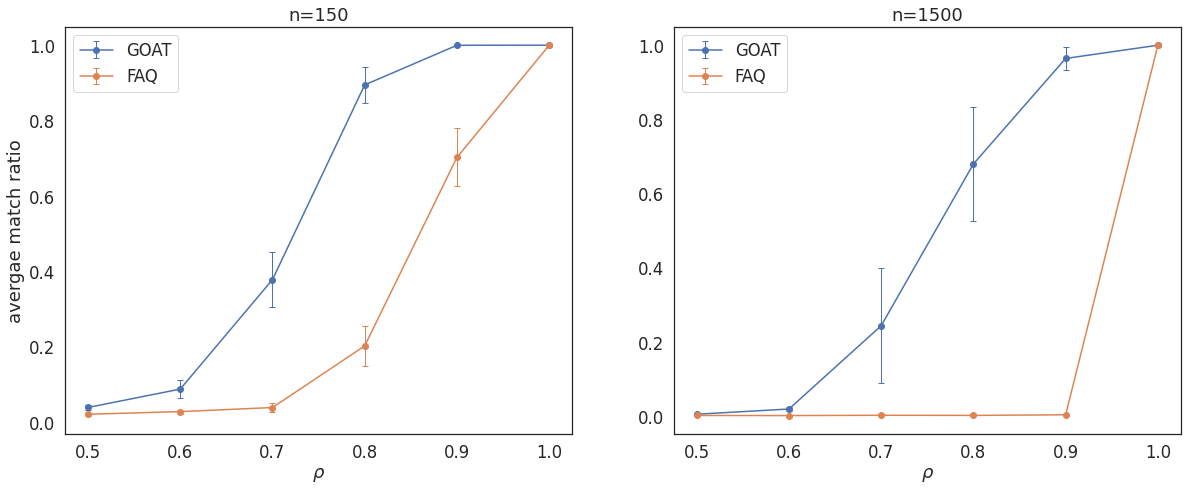
Caption:¶
Average match ratio \(\pm\) 2 s.e. as a function of correlation values \(\rho\) in \(\rho\)-SBM simulations on \(n=150, 1500\) nodes.
#collapse
from scipy.stats import sem
cb = ['#377eb8', '#ff7f00', '#4daf4a',
'#f781bf', '#a65628', '#984ea3',
'#999999', '#e41a1c', '#dede00']
error = [2*sem(ratios[i,:]) for i in range(n_p)]
average = [np.mean(ratios[i,:] ) for i in range(n_p)]
error_ss = [2*sem(ratios_ss[i,:]) for i in range(n_p)]
average_ss = [np.mean(ratios_ss[i,:] ) for i in range(n_p)]
sns.set_context('poster')
sns.set(rc={'figure.figsize':(15,10)})
sns.set(font_scale = 2)
sns.set_style('white')
# plt.set_cmap(CB_color_cycle)
sns.set_palette(sns.color_palette('colorblind'))
plt.errorbar(rhos,average_ss, error_ss,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GOAT', color=cb[0])
plt.errorbar(rhos,average, error,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='FAQ', color=cb[1])
plt.xlabel(r"$\rho$")
plt.ylabel("avergae match ratio")
plt.title('n=150')
plt.legend()
<matplotlib.legend.Legend at 0x7f96a1780978>
Experiment Summary, n = 1500¶
Let \((G_1, G_2) \sim \rho-SBM(\vec{n},B)\). (NB: binary, symmetric, hollow.)
\(K = 3\).
the marginal SBM is conditional on block sizes \(\vec{n}=[n_1,n_2,n_3]\).
\(B = [(.20,.01,.01);(.01,.10,.01);(.01,.01,.20)]\). (NB: rank(\(B\))=3 with evalues \(\approx [0.212,0.190,0.098]\).)
with \(n = 150\) and \(\vec{n}=[n_1,n_2,n_3] = [50,50,50]\)
for each \(\rho \in \{0.8, 0.85, 0.9, 0.95, 1.0\}\) generate \(r\) replicates \((G_1, G_2)\).
For all \(r\) replicates, run \(GM\) and \(GM_{LS}\) (where \(GM_{LS}\) uses the “Lightspeed sinkhorn distances” for computing the step direction) each \(t\) times, with each \(t\) corresponding to a different random permutation on \(G_2\) .
Specifically,\(G_2' = Q G_2 Q^T,\) where \(Q\) is sampled uniformly from the set of \(n x n\) permutations matrices.
For each \(t\) permutation, run \(GM\) & \(GM_{SS}\) from the barycenter (\(\gamma = 0\)).
For each \(r\), the \(t\) permutation with the highest associated objective function value will have it’s match ratio recorded
For any \(\rho\) value, have \(\delta\) denote the average match ratio over the \(r\) realizations
Plot \(x=\rho\) vs \(y\)= \(\delta\) \(\pm\) s.e.
Below contains figures for \(r=25\), \(t=5\)
#hide
import numpy as np
import matplotlib.pyplot as plt
import random
import sys
from joblib import Parallel, delayed
import seaborn as sns
# from graspy.match import GraphMatch as GMP
from graspologic.simulations import sbm_corr
# from scipy.optimize import linear_sum_assignment
from sklearn.metrics import pairwise_distances
r = 25
t=5
# gmp = GraphMatch('maximize':True, 'tol':0.000001,'maxiter':30, 'shuffle_input':True)
def match_ratio(inds, n):
return np.count_nonzero(inds == np.arange(n)) / n
n = 1500
m = r
rhos = 0.1 * np.arange(11)[5:]
# rhos = np.arange(8,10.5,0.5) *0.1
n_p = len(rhos)
ratios = np.zeros((n_p,m))
scores = np.zeros((n_p,m))
ratios_ss = np.zeros((n_p,m))
scores_ss = np.zeros((n_p,m))
n_per_block = int(n/3)
n_blocks = 3
block_members = np.array(n_blocks * [n_per_block])
block_probs = np.array([[0.2, 0.01, 0.01], [0.01, 0.1, 0.01], [0.01, 0.01, 0.2]])
directed = False
loops = False
for k, rho in enumerate(rhos):
np.random.seed(8888)
seeds = [np.random.randint(1e8, size=t) for i in range(m)]
def run_sim(seed):
A1, A2 = sbm_corr(
block_members, block_probs, rho, directed=directed, loops=loops
)
score = 0
res_opt = None
score_ss = 0
res_opt_ss = None
for j in range(t):
res = quadratic_assignment(A1,A2, options={'maximize':True, 'tol':1e-3,'maxiter':30, 'shuffle_input':True})
if res.fun>score:
perm = res.col_ind
score = res.fun
res_ss = quadratic_assignment_ot(A1,A2, options={'maximize':True, 'tol':1e-3,'maxiter':30, 'shuffle_input':True, 'reg': 100})
if res_ss.fun>score_ss:
perm_ss = res_ss.col_ind
score_ss = res_ss.fun
ratio = match_ratio(perm, n)
ratio_ss = match_ratio(perm_ss, n)
return ratio, score, ratio_ss, score_ss
result = Parallel(n_jobs=-1)(delayed(run_sim)(seed) for seed in seeds)
ratios[k,:] = [item[0] for item in result]
scores[k,:] = [item[1] for item in result]
ratios_ss[k,:] = [item[2] for item in result]
scores_ss[k,:] = [item[3] for item in result]
from scipy.stats import sem
error1500 = [2*sem(ratios[i,:]) for i in range(n_p)]
average1500 = [np.mean(ratios[i,:] ) for i in range(n_p)]
error_ss1500 = [2*sem(ratios_ss[i,:]) for i in range(n_p)]
average_ss1500 = [np.mean(ratios_ss[i,:] ) for i in range(n_p)]
sns.set_context('poster')
sns.set(rc={'figure.figsize':(15,10)})
sns.set(font_scale = 2)
sns.set_style('white')
plt.errorbar(rhos,average_ss1500, error_ss1500,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GOAT')
plt.errorbar(rhos,average1500, error1500,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='FAQ')
plt.xlabel(r"$\rho$")
plt.ylabel("avergae match ratio")
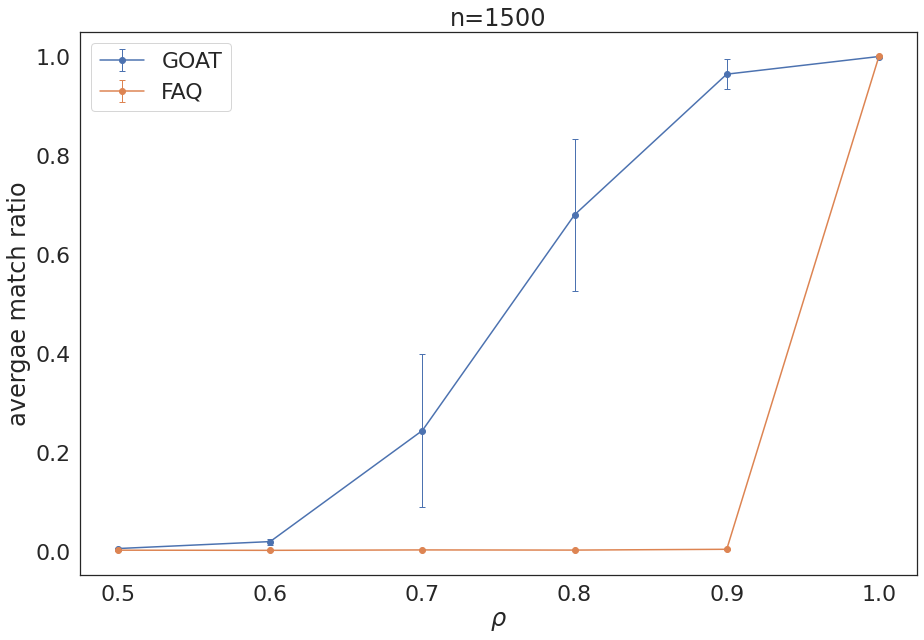
plt.title('n=1500')
plt.legend()
<matplotlib.legend.Legend at 0x7f96a151e160>
sns.set(font_scale = 1.5)
sns.set_style('white')
fig, axes = plt.subplots(1, 2, figsize=(20, 7.5))
rhos1 = 0.1 * np.arange(11)[5:]
axes[0].errorbar(rhos1,average_ss, error_ss,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GOAT')
axes[0].errorbar(rhos1,average, error,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='FAQ')
axes[0].set_xlabel(r"$\rho$")
axes[0].set_ylabel("avergae match ratio")
axes[0].set_title('n=150')
axes[0].legend()
axes[1].errorbar(rhos,average_ss1500, error_ss1500,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='GOAT')
axes[1].errorbar(rhos,average1500, error1500,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='FAQ')
axes[1].set_xlabel(r"$\rho$")
# plt.ylabel("avergae match ratio")
axes[1].set_title('n=1500')
axes[1].legend()
plt.savefig('sgm.png')
# axes[0].set_ylabel("average match ratio")
# for i in range(3):
# sns.set(font_scale = 2)
# sns.set_style('white')
# axes[i].errorbar(m,ratios[:, i], 2*error[:, i], fmt='.-',capsize=3, elinewidth=1, markeredgewidth=1, label='GOAT')
# axes[i].errorbar(m,ratios2[:, i], 2*error2[:, i],fmt='.-',capsize=3, elinewidth=1, markeredgewidth=1, label='FAQ')
# axes[i].legend(prop={'size': 15})
# axes[i].set_title(fr'$\rho$ = {np.around(rhos[i],2)}', fontsize=15)
# axes[i].set_xlabel("number of seeds (m)")
plt.savefig('rho_sbm.png')
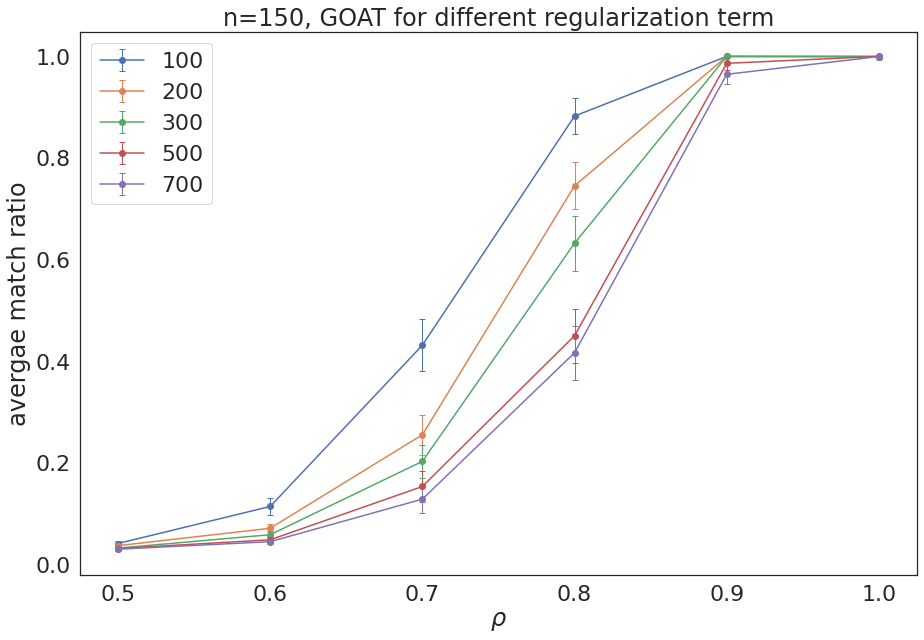
GOAT for different values of reg = [100, 200, 300, 500, 700]¶
#hide
import numpy as np
import matplotlib.pyplot as plt
import random
import sys
from joblib import Parallel, delayed
import seaborn as sns
# from graspy.match import GraphMatch as GMP
from graspologic.simulations import sbm_corr
# from scipy.optimize import linear_sum_assignment
from sklearn.metrics import pairwise_distances
r = 50
t=10
# gmp = GraphMatch('maximize':True, 'tol':0.000001,'maxiter':30, 'shuffle_input':True)
def match_ratio(inds, n):
return np.count_nonzero(inds == np.arange(n)) / n
n = 150
m = r
rhos = 0.1 * np.arange(11)[5:]
# rhos = np.arange(8,10.5,0.5) *0.1
n_p = len(rhos)
ratios_1 = np.zeros((n_p,m))
ratios_2 = np.zeros((n_p,m))
ratios_3 = np.zeros((n_p,m))
ratios_5 = np.zeros((n_p,m))
ratios_7 = np.zeros((n_p,m))
n_per_block = int(n/3)
n_blocks = 3
block_members = np.array(n_blocks * [n_per_block])
block_probs = np.array([[0.2, 0.01, 0.01], [0.01, 0.1, 0.01], [0.01, 0.01, 0.2]])
directed = False
loops = False
for k, rho in enumerate(rhos):
np.random.seed(8888)
seeds = [np.random.randint(1e8, size=t) for i in range(m)]
def run_sim(seed):
A1, A2 = sbm_corr(
block_members, block_probs, rho, directed=directed, loops=loops
)
score_1 = 0
score_2 = 0
score_3 = 0
score_5 = 0
score_7 = 0
# res_1 = None
# res_2 = None
# res_3 = None
# res_4 = None
# res_5 = None
def run_qap(reg):
score = 0
for j in range(t):
res = quadratic_assignment_ot(A1,A2, options={'maximize':True,'tol':1e-6,'maxiter':50, 'shuffle_input':True, 'reg': reg, 'thr':1e-2})
if res.fun>score:
perm = res.col_ind
score = res.fun
return perm
ratio_1 = match_ratio(run_qap(100), n)
ratio_2 = match_ratio(run_qap(200), n)
ratio_3 = match_ratio(run_qap(300), n)
ratio_5 = match_ratio(run_qap(500), n)
ratio_7 = match_ratio(run_qap(700), n)
return ratio_1, ratio_2, ratio_3, ratio_5, ratio_7
result = Parallel(n_jobs=-1)(delayed(run_sim)(seed) for seed in seeds)
ratios_1[k,:] = [item[0] for item in result]
ratios_2[k,:] = [item[1] for item in result]
ratios_3[k,:] = [item[2] for item in result]
ratios_5[k,:] = [item[3] for item in result]
ratios_7[k,:] = [item[4] for item in result]
from scipy.stats import sem
error_1 = sem(ratios_1, axis=1)
average_1 = np.mean(ratios_1, axis=1)
error_2 = sem(ratios_2, axis=1)
average_2 = np.mean(ratios_2, axis=1)
error_3 = sem(ratios_3, axis=1)
average_3 = np.mean(ratios_3, axis=1)
error_5 = sem(ratios_5, axis=1)
average_5 = np.mean(ratios_5, axis=1)
error_7 = sem(ratios_7, axis=1)
average_7 = np.mean(ratios_7, axis=1)
#sns.set_context('poster')
sns.set(rc={'figure.figsize':(15,10)})
sns.set(font_scale = 2)
sns.set_style('white')
# txt =f'r={r}, t={t}'
plt.errorbar(rhos,average_1, error_1,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='100')
plt.errorbar(rhos,average_2, error_2,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='200')
plt.errorbar(rhos,average_3, error_3,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='300')
plt.errorbar(rhos,average_5, error_5,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='500')
plt.errorbar(rhos,average_7, error_7,marker='o',capsize=3, elinewidth=1, markeredgewidth=1, label='700')
sns.color_palette('bright')
plt.xlabel(r"$\rho$")
plt.ylabel("avergae match ratio")
# plt.text(0.5,0.5,txt)
plt.title('n=150, GOAT for different regularization term')
plt.legend()
<matplotlib.legend.Legend at 0x7fdaacec2ba8>